Deformation field correction for spatial normalization of PET images using a population-derived partial least squares model
Deformation Field Correction for Spatial Normalization of PET Images Using a Population-derived Partial Least Squares Model
Murat Bilgel, Aaron Carass, Susan M. Resnick, Dean F. Wong, and Jerry L. Prince
Introduction
Deformable medical image registration is essential to aligning a population of images, performing voxelwise association studies, and tracking longitudinal changes. Anatomically accurate positron emission tomography (PET) spatial normalization is a difficult problem since they reflect metabolism and function rather than anatomy, and work on it remains limited. In this study, we present a method for the spatial normalization of PET images without a corresponding structural image based on a deformation correction model learned from structural image registration.
Method
Our method is based on this observation: “PET-to-PET registration produces deformations that are systematically biased in certain regions, and these biases can be characterized as a function of location and estimated within small neighborhoods.” The correction operates on the PET-to-PET deformation fields obtained from a deformable registration algorithm and uses partial least squares regression models learned from a population of subjects relating the local PET intensities and deformation fields to the corresponding structural imaging deformation fields. The learned relationship between the deformation fields accounts for the anatomical inaccuracies present in the alignment of PET images, while the use of PET intensity information allows for inter-subject variability in radio tracer binding due to differences in physiology.
To construct our model, we need the deformation fields that are to be applied to the PET images and their structural counterparts to bring the images to a common template. Our model is then trained using the resulting deformation fields for the PET and the structural images as well as the warped PET image intensities, yielding a correction that can be applied to PET deformation fields.
The process starts with image template generation. To create an automatically accurate PET template image, we rely on the associated structural images. The structural images are co-registered rigidly with the subject PET images. We then use the template building tool available in the ANTS package to construct a structural image template from the co-registered structural images [B. B. Avants et al. 2010]. The mappings obtained from the structural image template construction are applied to the corresponding PET images in order to bring them into the same template space. The PET template is then defined as the mean of the spatially normalized PET images.
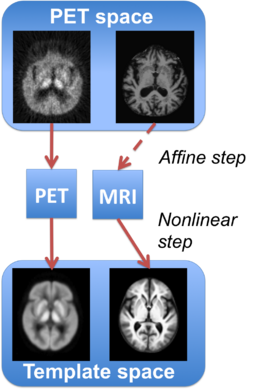
We next compute a training set. Using a set of subjects for whom both a structural image and a PET image are available, we perform deformable registration to map the PET images onto the PET template. For each subject in the training data, the deformable registration consists of an affine transformation followed by a diffeomorphic mapping. Constraining the affine transformation to be the same as that obtained from the PET-to-PET registration, we perform another registration to find the deformation field that must be applied to the structural image. A diagram of this registration scheme is presented in Figure 1. We used SyN registration for our experiments [B. B. Avants et al. 2008].
We then perform model training. The goal is to train a model at each voxel that describes a relationship between the estimated PET deformation field and the structural image deformation field. We use the PET deformation vectors and image intensities within a 3x3x3 neighborhood as input features, and the output is the structural image deformation vector at the center voxel. We apply the partial least squares (PLS) dimensionality reduction technique to the training data. The number of components to keep is chosen using cross-validation on the training set. The final model is a partial least squares regression model that can be used to predict the structural image deformation field given a PET deformation field.
Results
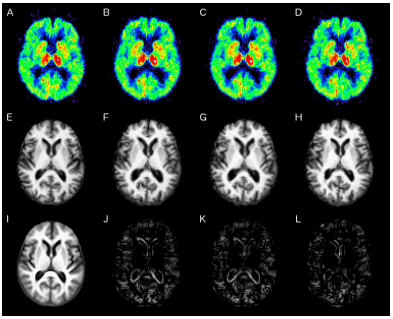
We compared our method against the PET-to-PET template registration and an implementation of [J. Fripp et. al.] that involved modifying the PET template according to a whole-brain PCA model following an affine registration of the subject’s PET and using the modified template to perform the deformable registration. Ventricle size is overestimated in both the PET-to-PET method as well as the method described in [J. Fripp et. al.], but our method results in a better registration as shown in the difference image (Figure 2). The putamen, a structure that exhibits higher activity in the PET image and thus causes spillover, is also better aligned by our method.
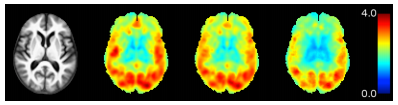
In Figure 3 we show a comparison of the root mean square (RMS) error of the deformation fields. Our method achieves the lowest overall RMS error.
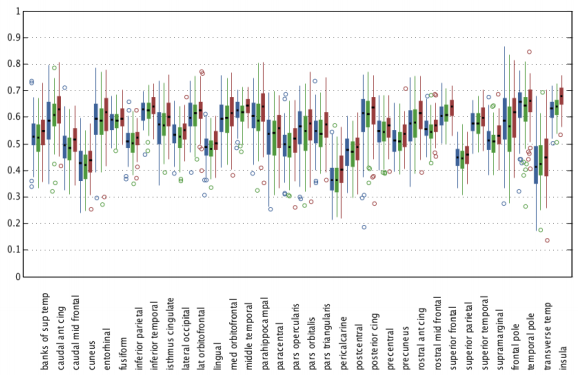
To assess the accuracy of anatomical alignment, the FreeSurfer [R.S. Desikan et al.] segmentations of the original MPRAGE images were brought into the template space by applying the mappings from the previously performed registrations. Using the FreeSurfer labels, we calculated the Dice coefficients [L.R. Dice et al.]. Table 1 shows the summary statistics for Dice coefficients for major brain tissue types and Figure 3 shows the Dice coefficient box plots for cortical regions. Our method consistently achieves higher Dice coefficients than either of the methods compared against.
Conclusion
We presented a deformation correction method that can improve the anatomical alignment of PET images in PET-to-PET registration. Cross validation results show that our deformation correction method reduces the deformation field error and improves the anatomical alignment of PET images as evidenced by the higher Dice coefficients calculated using the deformed segmentations.
The improvement in anatomical alignment across multiple brain regions achieved by our method points to the systematic errors present in PET-to-PET registration. Our method can compensate for such errors present in PET-to-PET registration by learning locally from the structural image registrations. While we used SyN for registration purposes, the presented method can be applied to any deformable PET-to-PET registration method.
Publications
- A. Carass, J. Cuzzocreo, M.B. Wheeler, P.L. Bazin, S.M. Resnick, J.L. Prince, "Simple paradigm for extra-cerebral tissue removal: algorithm and analysis", NI, 56(4):1982-1992, 2011.
References
- B. B. Avants, C. L. Epstein, M. Grossman, J. C. Gee, "Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain.", Medical Image Analysis, 12(1): 26-41, 2008.
- B. B. Avants, P. Yushkevich, J. Pluta, D. Minkoff, M. Korczykowski, J. Detre, J. C. Gee, "The optimal template effect in hippocampus studies of diseased populations", NeuroImage, 49(3): 2457-66, 2010.
- J. Fripp, P. Bourgeat, O. Acosta, G. Jones, V. Villemagne, S. Ourselin, C. Rowe, O. Salvado, "Generative atlases and atlas selection for C11-PIB PET-PET registration of elderly mild cognitive impaired and Alzheimer disease patients", Fifth IEEE International Symposium on Biomedical Imaging (ISBI 2008), Paris, France, May 14-17, 2008.
- L.R. Dice, "Measures of the amount of ecologic association between species", Ecology, 26(3): 297-302, 1945.
- R.S. Desikan, B. Fischl, B.T. Quinn, B.C. Dickerson, D. Blacker, R.L. Buckner, A.M. Dale, R.P. Maguire, B.T. Hyman, M.S. Albert, R.J. Killiany, "An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest", NI, 31(3):968-980, 2006.