Analysis of macular OCT images using deformable registration
<meta name="title" content="Analysis of Macular OCT images using deformable registration"/>
Analysis of Macular OCT images using deformable registration
Min Chen, Andrew Lang, Howard S. Ying, Peter A. Calabresi, Jerry L. Prince, and Aaron Carass
Introduction
Optical coherence tomography (OCT) of the macula has become increasingly important in the investigation of retinal pathology. However, deformable image registration, which is used for aligning subjects for pairwise comparisons, population averaging, and atlas label transfer, has not been well developed and demonstrated on OCT images. In this paper, we present a deformable image registration approach designed specifically for macular OCT images.
Methods
Initial Preprocessing happens prior to performing the OCT registration, our method requires two initial preprocessing steps that are applied to the OCT images. First we apply an intensity normalization process to each OCT volume. Second, we estimate and mask the images to the retinal boundaries by locating the inner limiting membrane (ILM) and Bruch’s membrane (BrM), which also serve as landmarks for our affine registration step.
We then start the image registration. The primary goal of image registration is to estimate a transformation that maps corresponding locations between a subject image and a target image. The two major challenges of retinal OCT registration are that the image voxels tend to be highly anisotropic and that the physical geometry of the image is not properly defined by how the A-scans are presented in the OCT.
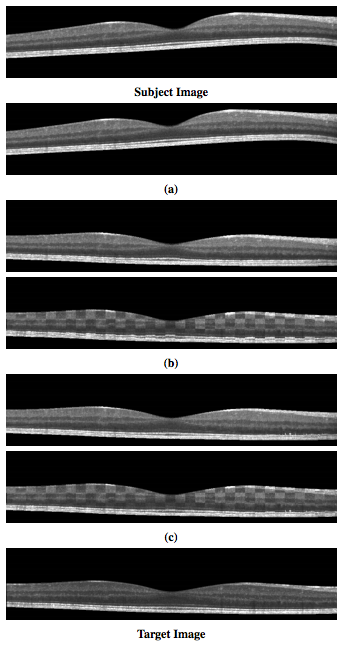
To address these concerns, we impose strong restrictions on the class of transformations our registration is allowed to estimate. In the x(lateral) and y(through plane) directions, we permit only discrete translations such that A-scans from the subject always coincide with A-scans in the target. This removes the need to interpolate intensities between two A-scans or two B-scans. Non-rigid transformations are only allowed in the z (axial) direction and will be constructed as a composition of individual (A-scan to A-scan) affine and deformable registration steps. This will permit accurate alignment of the features in each A-scan, including the retinal layers. Our overall registration result is the composition of three steps: a 2D global translation of the whole volume (using discrete offsets only), a set of 1D affine transformations applied to each A-scan, and a set of ID deformable transformations applied to each A-scan. These transformations are learned and applied in stages and then composed t construct the total 3D transformation.
Construction a normalized space using a deformable registration is next. An important application of deformable registration is the ability to construct a normalized space for analyzing a population of subjects are registered. This allows spatial correspondences between the subjects to be observed and analyzed together as a population. Often, an average atlas is constructed for this purpose, where the atlas represents the average anatomy of the population. Constructing such an atlas and using it as a normalized space via deformable registration is a well studied topic in brain MRI analysis. We use a method where the average atlas is found by iteratively registering each subject to an estimate of the average atlas, and then adjusting the atlas such that the average of all the deformations is closer to zero.
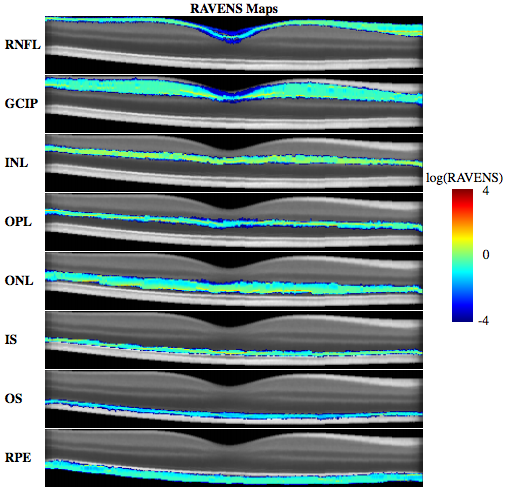
We then begin regional analysis of volumes examined in normalized space. The ability to construct a normalized space opens up numerous existing techniques for analyzing images from a population perspective. To demonstrate this capability, we apply our registration approach in conjunction with the tissue density based analysis known as RAVENS [A.F. Goldszal et. al.]. RAVENS uses tissue segmentation with the deformation learned from each registration to the normalized space to estimate the relative local volume changes between each subject and the atlas. The relative local volume change is calculated by first taking each voxel in a segmentation and projecting it into the target space using the registration deformation fields. This process keeps track of how each voxel is distributed by the projection and allows the method to record the degree of compression and expansion at each voxel that the segmentations had to undergo in order to be registered into the normalized space. As a result, we obtain localized measures of volume changes for each subject relative to the average atlas. This provides the ability to locate differences in relative volume changes between control and disease populations.
|
|
Materials
We use two pools of data for the various experiments and comparisons in the remainder of the paper.
We used a Validation cohort consisting of OCT images of the right eyes from 45 subjects, 26 diagnosed with MS with 19 as healthy controls. An internally developed protocol was used to manually label nine layer boundaries on all B-scans for all subjects. These nine boundaries partition an OCT data set into eight regions of interest.
- Retinal nerve fiber layer (RNFL)
- Ganglion cell layer and inner plexiform layer (GCIP)
- Inner nuclear layer (INL)
- Outer plexiform layer (OPL)
- Outer nuclear layer (ONL)
- Inner segment (IS)
- Outer Segment (OS)
- Retinal pigment epithelium (RPE)
These retinal layers are used to demonstrate the accuracy of our registration method, by comparing the algorithm’s ability to use the learned deformation to transfer known labels in the subject to an unlabeled target image.
Our general cohort consists of retinal image from 83 subjects, all right eyes with 43 MS patients and 40 controls. Layer segmentations for this cohort was generated automatically using a boundary classification and graph based method [A. Lang et. al.], which has been shown as highly reliable. The data collection is used to demonstrate several applications of our deformable registration and normalized space.
Applications
We use two pools of data for the various experiments and comparisons in the remainder of the paper.
We used a Validation cohort consisting of OCT images of the right eyes from 45 subjects, 26 diagnosed with MS with 19 as healthy controls. An internally developed protocol was used to manually label nine layer boundaries on all B-scans for all subjects. These nine boundaries partition an OCT data set into eight regions of interest.
Retinal nerve fiber layer (RNFL) Ganglion cell layer and inner plexiform layer (GCIP) Inner nuclear layer (INL) Outer plexiform layer (OPL) Outer nuclear layer (ONL) Inner segment (IS) Outer Segment (OS) Retinal pigment epithelium (RPE)
These retinal layers are used to demonstrate the accuracy of our registration method, by comparing the algorithm’s ability to use the learned deformation to transfer known labels in the subject to an unlabeled target image.
Discussion and Conclusion
|
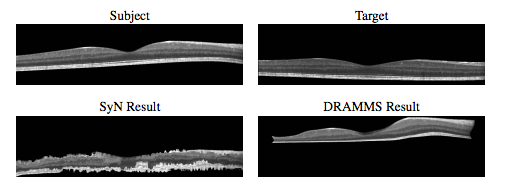
To our knowledge, there has been no other openly available deformable registration algorithm designed and validated on macular OCT volumes. Hence, our method could only be compared against currently available generic registration algorithms that have been used with success in various other anatomical locations. Our results in Table 1 and 2 show that on average our D-OCT algorithm produced the most accurate and robust results for aligning retinal layers when comparing segmentations transferred by the registration against manual segmentations. Using our registration approach, we have constructed a normalized space and average atlas for macular OCT, which enables a number of population based analysis. In this work, we’ve shown two such applications. First, we have created a set of statistical atlases, which can be used as prior information for future segmentation and registration approaches. This allows such algorithms to improve its accuracy by comparing unknown images to these atlases in order to create robust initializations for the solution. These atlases can also potentially be used to develop more advanced atlases for comparison against normal anatomy, similar to standard growth charts. Second, we used the normalized space to perform population analysis by constructing RAVENS maps to analyze local volume differences between controls and patients with MS. Our results found significant clusters of volume change difference between healthy and MS patients in the RNFL and GCIP layer.However, one major advantage provided by our analysis is the ability to detect specifically in 3D where such changes are occurring, whereas previous methods relied on average OCT thickness analysis across 2D regions of the macula or post-mortem histological analysis.This type of analysis is unavailable when using standard approaches for evaluating macular OCT.
We have presented both an affine and deformable registration method designed specifically for OCT images of the macula, which respect the acquisition physics of the imaging modality. Our validation using manual segmentations shows that our algorithm is considerably more accurate and robust for aligning retinal layers than existing generic registration algorithms. Our method opens up a number of applications for analysis of OCT that were previously not available. We have demonstrated three such examples through the creation of an average atlas, a statistical atlas, and a pilot study of local volume changes in the macula of healthy controls and MS patients. However, these are but a small example of the existing methods and techniques that utilize deformable registration and normalized spaces to perform population based analysis of health and disease.
Acknowledgments
This work was supported by the NIH/NEI under grant R21-EY022150, NIH/NINDS R01-NS082347, and the Intramural Research Program of NINDS.
Publications
- M. Chen, A. Lang, H.S. Ying, P.A. Calabresi, J.L. Prince, and A. Carass, "Analysis of macular OCT images using deformable registration", Biomedical Optics Express, 5(7):2196-2214, 2014. (doi)
- A. Lang, A. Carass, E. Sotirchos, and J.L. Prince, "Segmentation of retinal OCT images using a random forest classifier", Proceedings of SPIE Medical Imaging (SPIE-MI 2013), Orlando, FL, February 9-14, 2013.
- A. Lang, A. Carass, M. Hauser, E.S. Sotirchos, P.A. Calabresi, H.S. Ying, and J.L. Prince, "Retinal layer segmentation of macular OCT images using boundary classification", Biomedical Optics Express, 4(7): 1133-1152, 2013. (PubMed)
- M. Chen, A. Lang, E. Sotirchos, H.S. Ying, P.A. Calabresi, J.L. Prince, and A. Carass, "Deformable registration of macular oct using a-mode scan similarity", Tenth IEEE International Symposium on Biomedical Imaging (ISBI 2013), San Francisco, CA, April 7 - 11, 2013.
- M. Chen, A. Carass, D. Reich, P. Calabresi, D. Pham, and J.L. Prince, "Voxel-wise displacement as independent features in classification of multiple sclerosis", Proceedings of SPIE Medical Imaging (SPIE-MI 2013), Orlando, FL, February 9-14, 2013.
- B.C. Lucas, J.A. Bogovic, A. Carass, P.-L. Bazin, J.L. Prince, D.L. Pham, and B.A. Landman, "The Java Image Science Toolkit (JIST) for rapid prototyping and publishing of neuroimaging software", Neuroinformatics, 8(1):5-17, 2010. (PubMed)
References
- A.F. Goldszal, C. Davatzikos, D. Pham, M.X.H. Yan, R.N. Bryan and S.M. Resnick, "An image processing system for qualitative and quantitative volumetric analysis analysis of brain images", Journal of Computer Assisted Tomography, 22(5):827-837, 1998.
- B.B. Avants, C.L. Epstein, M. Grossman, and J.C. Gee, "Symmetric diffeomorphic image registration with cross correlation: Evaluationg automated labeling of elderly and neurodegenerative brain", Medical Image Analysis, 12(1):26-41, 2008.
- A. Klein, S.S. Ghosh, B. Avants, B.T.T. Yeo, B. Fischl, B. Ardekani, J.C. Gee, J.J. Mann, and R.V. Parsey, "Evaluation of volume-based and surface-based brain image registration methods", NeuroImage, 2010.