Automatic method for thalamus parcellation using multi-modal feature classification
<meta name="title" content="Automatic method for thalamus parcellation using multi-modal feature classification"/>
Automatic method for thalamus parcellation using multi-modal feature classification
Joshua V. Stough, Jeffrey Glaister, Chuyang Ye, Sarah H Ying, Jerry L. Prince, and Aaron Carass
Introduction
Segmentation and parcellation of the thalamus is an important step in providing volumetric assessment of the impact of disease weighted magnetic resonance (MR) images and nuclear parcellation using diffusion weighted MR images. In this work we present the first fully automatic method that incorporates both tissue contrasts and several derived features to the first segment and then parcellate the thalamus.
Method
The first thing that happens is ROI identification. In order to reduce the computational burden of training an RF we estimate bounding boxes for the left and right thalami. These ROIs are identified using a tissue segmentation and labeling approach based on topology preservation and fuzzy classification [Bazin and Pham]. Next are Knutsson space and edge maps. DTI is acquired from diffusion weighted MRI, using a gradient spin echo pulse sequence with a known b-value b and gradient direction g.
What this process results in is an edge map representing a change in the direction of the PEV, which will allow us to distinguish thalamic nuclei.
Then the connectivity to the cortical mantle is calculated. This is calculated using probabilistic tractography implemented in the FSL toolkit. Six cortical masks corresponding to thalamic connection sites are used as the targets for the tractography algorithm.![]() is the set of voxels in a cortical mask and
is the set of voxels in a cortical mask and ![]() is the cortical mask label. The six labels for the cortical masks are {frontal, occipital, parietal, temporal, precentral, postcentral}. Connectivity
is the cortical mask label. The six labels for the cortical masks are {frontal, occipital, parietal, temporal, precentral, postcentral}. Connectivity ![]() is defined as the number of times a sample starting at the voxel x forms a pathway connecting to any voxel y belonging to the cortical mask with label
is defined as the number of times a sample starting at the voxel x forms a pathway connecting to any voxel y belonging to the cortical mask with label ![]() ,
,
5000 samples are initiated per voxel in B and the path direction is determined by local fiber directions.
This process uses a Random Forest Framework. The first features input into our RF framework are the relative position of ![]() and the MR intensity value at
and the MR intensity value at ![]() ,
, ![]() . These intensities provide clues about the boundary of the thalamus with non-thalamus structures. The core distinguishing features of the nuclear groups are fiber orientation and strength. Thus the next set of features are FA, MD, Knutsson mapping, and Frobenius norm. These features ultimately give us an 18-dimensional feature space.
. These intensities provide clues about the boundary of the thalamus with non-thalamus structures. The core distinguishing features of the nuclear groups are fiber orientation and strength. Thus the next set of features are FA, MD, Knutsson mapping, and Frobenius norm. These features ultimately give us an 18-dimensional feature space.
Our hierarchical RF [Breiman] approach uses ![]() for each voxel in the available training data to build a collection of trees that first distinguishes the thalamus within
for each voxel in the available training data to build a collection of trees that first distinguishes the thalamus within ![]() from other tissues. This is a binary classification task identifying thalamus from background. A second RF is then built using the same feature vector, trained to provide a membership for each of the sic thalamic nuclear groups given that we know the thalamus from the first stage. The first stage thalamus identification can be quite noisy due to peripheral objects have a thalamus-like appearance. To reduce this artifact, we select the largest connected component foreground object which we then close with a 3x3x3 structuring element. The RFs can be applied to a new subject, with classification scores determining the segmentation of the thalamus and subsequent parcellation of the nuclear groups.
from other tissues. This is a binary classification task identifying thalamus from background. A second RF is then built using the same feature vector, trained to provide a membership for each of the sic thalamic nuclear groups given that we know the thalamus from the first stage. The first stage thalamus identification can be quite noisy due to peripheral objects have a thalamus-like appearance. To reduce this artifact, we select the largest connected component foreground object which we then close with a 3x3x3 structuring element. The RFs can be applied to a new subject, with classification scores determining the segmentation of the thalamus and subsequent parcellation of the nuclear groups.
Results
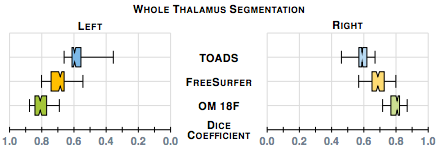
Our first results compare our estimate of the thalamus with those from two whole brain segmentation software tools [1,9]. We used leave-one-out cross-validation runs and Dice scores are shown in figure 1. A paired Wilcoxon rank sum test comparing our method with Bazin and Pham (TOADS) had a p-value < 0.001 for both the left and right thalami (computed independently) indicating significant improvement. A similar test between our method and Dale et. al. FreeSurfer) gives a p-value < 0.001 for the right thalamus; however for the left thalamus the p-value is 0.00684, which is just shy of statistical improvement.
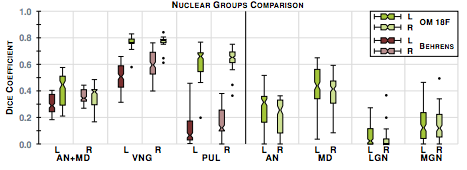
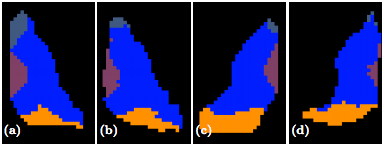
The second step in our hierarchical RF framework distinguishes thalamic nuclei assuming that the thalamus boundary is known from the first stage. To test, we have also implemented an automated algorithm based on Behrens et. al. which used only the cortical labels to parcellate the thalamus. The fiber groupings in Behrens et. al. are different to ours thus for comparison we merged AN & MD. Behrens et. al. also excluded LGN and MGN from their parcellation. The comparable nuclear groups are shown in figure 2 as well as the additional groups we can parcellate. We also have examples of our parcellation of two subjects in figure 3.
|
|
Conclusion
In this paper we have presented the first fully automatic thalamic parcellation method using multi-modal imaging data, and we make two important contributions. Firstly we use a multi-channel framework to segment the thalamus, the first such method. Secondly, we provide a parcellation of the six core nuclear groups of the thalamus in a fully automated fashion.
References
- P.L. Bazin and D.L. Pham, "Homeomorphic brain image segmentation with topological and statistical atlases", Medical Image Analysis, 12(5): 616-625, 2008.
- T.E.J Behrens et. al., "Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging", Nature Neuroscience, 6(7): 750-757, 2003.
- L. Breiman, "Random Forests", Machine Learning, 45(1): 5-32, 2001.
- A.M. Dale et. al., "Cortical Surface-Based Analysis I: Segmentation and Surface Reconstruction", NeuroImage, 9(2): 179-194, 1999.