Determining Functional Units of Tongue Motion via Graph-regularized Sparse Non-negative Matrix Factorization
Determining Functional Units of Tongue Motion via Graph-regularized Sparse Non-negative Matrix Factorization
Jonghye Woo, Fangxu Xing, Junghoon Lee, Maureen Stone, Jerry L. Prince
Introduction
The relationship between the structural and functional components of the tongue is poorly understood partly due to complex tongue anatomy and muscle interactions. Despite advances that have been made due to tMRI studies on understanding internal tissue motion, there has been very little research on its analysis to determine functional units. Motion clustering during tongue motion can be used to reveal the tongue’s intrinsic functional organization. In this work we assume a Riemannian manifold of the data within an NMF approach, which thereby captures the intrinsic geometric of the motion features derived from tMRI. In paticular, we propose a new approach to determine functional units of tongue motion from tMRI using graph-regularized sparse NMF with spectral clustering, termed GS-NMF-S.
Method
Consider a set of P internal tongue tissue points each with n scalar quantities tracked through F time frames. These quantities characterized each point and are used to group them into functional units. The location of the p-th tissue point at the f-th time frame can be writtens as (![]() ). The tongue motion can the be represented by
). The tongue motion can the be represented by ![]() spatio-temporal feature matrix
spatio-temporal feature matrix ![]()
![]() , where the p-th column is given by
, where the p-th column is given by
|
|
We cast the problem of determining the functional units as motion clustering problem. Thus the goal is to determine a permutation of the columns to form ![]() , where the submatrix
, where the submatrix ![]() comprises point tracks associated with the i-th submotion, i.e. the i-th functional unit. The overall algorithm is shown below:
comprises point tracks associated with the i-th submotion, i.e. the i-th functional unit. The overall algorithm is shown below:
|
Results
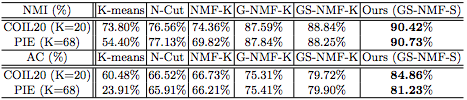
We used 2D datasets to demonstrate the clustering performance of the proposed method. In order to compare the performance of the different algorithms, we used a K-means clustering method (K-means), a normalized cut method (N-Cut) [Shi et. al.], standard NMF with K-means clustering (NMF-K), graph-regularized NMF with K-means clustering (G-NMF-K) [Cai et. al.], graph regularized sparse NMF with K-means clustering (GS-NMF-K) and our method (GS-NMF-S). The metrics we used to measure the performance of these algorithms are the Normalized Mutual Information (NMI) and the Accuracy (AC). Table 1 lists these values for all the algorithms.
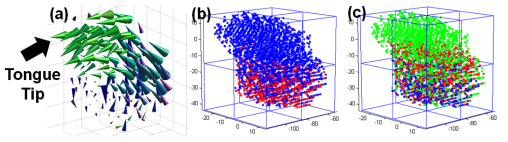
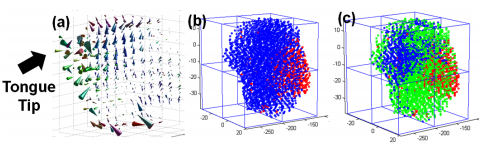
We also tested our method using a simple non-speech protrusion task and a speech task. Figure 1 shows the protrusion task and figure two shows part of the speech task. Note that the three clusters better represent the motions of the tongue. These motions include the backward motion of the tongue tip (blue), upward motion of the tongue body (green) and forward motion of the posterior tongue (red).
|
|
Conclusion
In this work we presented a novel method for determining functional units from tMRI. Unlike previous algorithms, this one aims at identifying the internal, coherent manifold structure of high-dimensional motion data to determine functional units. The proposed method gives a principled method for defining subject/task-specific functional units, which can be potentially used to elucidate speech-related disorders.
Publications
- V. Parthasarathy, J.L. Prince, M. Stone, E.Z. Murano, and M. NessAiver, "Measuring tongue motion from tagged cine-MRI using harmonic phase (HARP) processing", The Journal of the Acoustical Society of America, 121(1): 491-504, 2007.
- M. NessAiver and J.L. Prince, "Magnitude image CSPAMM reconstruction (MICSR)", Magnetic resonance in medicine, 50(2):331-342, 2003.
- F. Xing, J. Woo, E.Z. Murano, J. Lee, M. Stone, and J.L. Prince, "3D tongue motion from tagged and cine MR images", Medical Image Computing and Computer-Assisted Intervention Springer, 41-48, 2013.
References
- J. Shi, and J. Malik, "Normalized cuts and image segmentation", IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8): 888-905, 2000.
- D. Cai, X. He, J. Han, and T.S. Huang, "Graph regularized nonnegative matrix factorization for data representation", IEEE Transaction on Pattern Analysis and Machine Intelligence, 33(8): 1548-1560, 2011.