MGDM
<meta name="title" content="Multiple-object Geometric Deformable Model"/>
A Multiple Object Geometric Deformable Model for Image Segmentation
John A. Bogovic, Jerry L. Prince, and Pierre-Louis Bazin
Abstract
Deformable models are widely used for image segmentation, most commonly to find single objects within an image. Although several methods have been proposed to segment multiple objects using deformable models, substantial limitations in their utility remain. This paper presents a multiple object segmentation method using a novel and efficient object representation for both two and three dimensions. The new framework guarantees object relationships and topology, prevents overlaps and gaps, enables boundary-specific speeds, and has a computationally efficient evolution scheme that is largely independent of the number of objects. Maintaining object relationships and straightforward use of object-specific and boundary-specific smoothing and advection forces enables the segmentation of objects with multiple compartments, a critical capability in the parcellation of organs in medical imaging. Comparing the new framework with previous approaches shows its superior performance and scalability.
Introduction
In this paper, we present a multiple object geometric deformable model (MGDM) segmentation framework that (1) guarantees no overlaps or gaps (2) evolves only a few level set-derived functions independently of the number of regions, (3) can apply any existing type of speed in the level set literature, (4) can enforce relationships and topological constraints on any or all objects and groups of objects if desired, and (5) can apply speeds that are different according to the specific object-to-object boundary. In this framework, the evolution of the level set functions representing any number of objects or compartments is recast into the evolution of a fixed, small number of distance functions and an equal number of corresponding label functions. Only two or three distance functions are needed for two dimensional (2D) or three dimensional (3D) problems, respectively. Since the number of functions is fixed, the computational penalty for increasing the number of objects is small.
MGDM is a multi-object extension to the conventional geometric level set formulation, and therefore one can apply all the conventional speeds that are useful and familiar to the community and can employ all the conventional fast computational methods such as fast marching and the narrow band method. The problem of object overlaps and gaps is automatically solved because the evolving functions directly provide a partition of the image. Object labels are specifically tracked within the evolution, enabling the straightforward implementation object-dependent speeds, including different boundaries between specific objects or regions. The topology of objects and the relationships between groups of objects are preserved by using a multi-object simple point constraint directly on the new functions without having to reconstruct the level set function of individual objects. The description of MGDM we provide here is valid for both two-dimensional (2D) and three dimensional (3D) images, and is generalizable to higher dimensions.
Methods
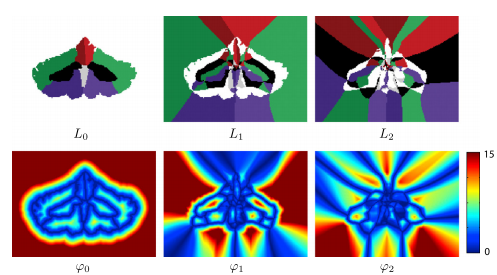
Decomposition of multiple level sets: We start with a decomposition of multiple level sets. First thing we do is define a set of label functions that describe the local configuration of neighboring objects. The label functions give a detailed description of the configuration of the objects. Then we use the label functions to define the related distance functions which specify the additional distances one must travel to reach the succession of the next-closet neighbors. Using both the label and distance functions, we then recover the signed distance function. Because we need all the label and distance functions, there is no apparent advantage to the proposed decomposition. But the key to realizing the advantages of the label-distance decomposition is to observe that only signed distance values near object boundaries are required to accurately carry out the geometric level set computations. We do not need to keep higher-order terms in this decomposition in order to carry out geometric deformable model computations.
|
Recovery of signed distance functions: Alternate distance for topology control: In applications where topology and relationships of segmented objects must be preserved, the process can be modified to reflect the fact that objects that are not in contact will never meet at a boundary. This means that the set of possible neighbors for a given object are restricted to the subset of labels in contact with the object.
Computing the level set decomposition and reinitialization: Like conventional level set methods, MGDM requires an initialization of the labels to be segmented in order to compute the truncated MGDM decomposition. the initialization often takes the form of a voxel-wise segmentation but can also make use of sub-grid information if level set functions of each object are provided. The computational complexity of this re-initialization scheme is lower than that of both the N level set method and the multiphase level set method, and it is not dependent on the number of objects. Our algorithm requires re-initialization of the distance functions during evolution for reasons similar to classical level set methods. Efficient computation of the decomposition is particularly important as this re-initialization involves the entire image rather than just the narrow band. After this step there is an evolution step in which the goal is to recast the evolution of any individual level set (this step is fleshed out in the full journal article).
Boundary-specific speeds: So far, the described framework has followed the classical approach where speeds are specified to act on objects. Some segmentation tasks would benefit from the ability to specify speeds that act on different parts of an object. In particular, there are scenarios in which we would prefer to specify the speeds of contours/surfaces between objects rather than the objects themselves. In this way, different parts of a single object can behave differently because they belong to different boundary surfaces. The MGDM framework directly encodes specific boundaries within its decomposition. The closest boundary is immediately identified , so therefore boundary specific speeds can be implemented without an expensive search for the closest boundary at each point.
Topology control: Topology control is often desired in medical imaging applications since the topology of organs and their relationships are known from human anatomy. Other applications may also benefit from prior knowledge of topology and/or relationship information of objects in the image or scene. Most methods for handling topology only maintain or correct the topology for one object, but do not control the topological relationships between objects. Digital homeomorphism [P.-L. Bazin et. al.] accounts for both single and multiple object constraints by controlling the topology of the boundary between objects. The level set decomposition we use intrinsically models boundary geometry and so digital homeomorphism constraints are incorporated very naturally. Multiple-object topology preservation usually requires the use of a template with the desired topology when initializing the level set evolution. The template is then registered to the image of interest in order to provide a topologically correct initialization. With topology control, objects can only come in contact if they are adjacent in the original template. Thus we can use an alternate distance definition in the algorithm and make the evolution more efficient by only considering topologically consistent candidates at a given point. The reinitialization is also faster as the marching can stop when an objects boundary reaches labels that are topologically invalid.
Experiments
|
|
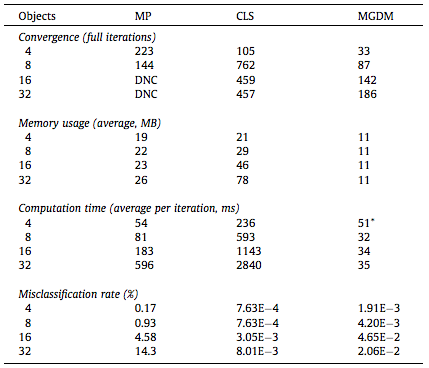
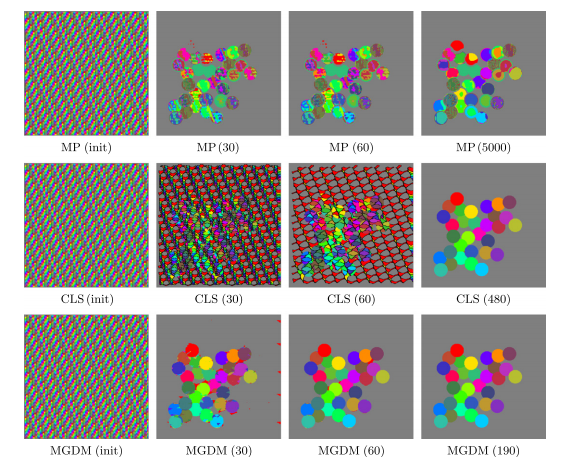
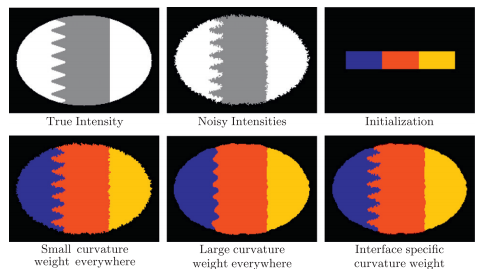
We compared our algorithm (MGDM), the multiphase approach (MP) and the N coupled level sets (CLS) of Brox and Weickert [24]. Rather than focusing on a specific application, we present a generic problem for which all methods should perform similarly given the same energy function. We test each method with four images and all methods converge correctly (shown in table 1). The MP method becomes plagued by local minima in it’s optimization, and while the CLS method avoids this but gaps do appear over the course of its evolution. MGDM remains stable while increasing the number of objects and also converges faster to the stable solution. The presence of gaps in CLS slows the apparent decrease of energy, while the optimization scheme of MP prevents it from reaching an energy as low as MGDM or CLS. We also wanted to demonstrate MGDM’s ability to apply speeds on object boundaries rather than on the objects themselves. Figure 4 shows the benefits of designing speeds for boundaries rather than objects. The central (red) object shares two boundaries with non-background objects with one boundary having a high curvature and one having a low curvature. We wanted to recover the locations of the boundaries after the have been corrupted by “boundary noise”. If curvature terms are applied uniformly on the central object, either the low curvature boundary will be overly noisy or the high curvature boundary will be overly smoothed. But we allow the curvature weights to to vary, so the influence of regularization and image terms can be balanced appropriately
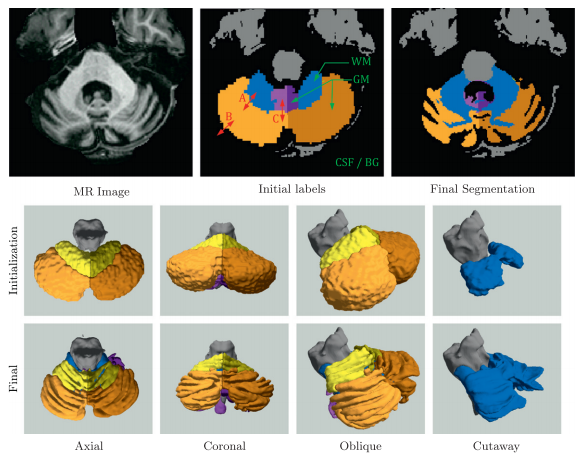
We also explored applying MGDM in the segmentation and parcellation of the cerebellum from structural MRI. A magnetization prepared rapid gradient echo (MP-Rage) image was acquired. The cerebellum has a central white matter (WM) structure called the corpus medullare from which white matter branches sprout. These branches are covered in a sheet of gray matter (GM) and together, form the cerebellar lobes and lobules. A good delineation of the corpus medullare (WM) should be smooth and not contain branches of white matter, which suggests that a strong curvature term is required. The cerebellar gray matter surface, on the other hand, is highly convoluted and suggests that a curvature should play a minor role at the boundary of gray matter and cerebral spinal fluid (CSF). Furthermore, while image intensity can separate cerebellar gray matter, white matter and CSF, the lobes themselves have similar intensities and are separated by thin line of lower intensity (and fissures).
Figure 5 shows an example of a cerebellum parcellation using MGDM. We observe the effective delineation of the tissue classes based on intensity. Note the simultaneous smoothness of the GM-WM boundary and the roughness of the GM-CSF boundary. The lobe boundaries are also well aligned with the fissures under the guidance of GVF.
|
|
Discussion
MGDM has shown strong and efficient results. It is well-suited to many new and challenging segmentation problems since it accurately and efficiently can represent many objects. We demonstrated here its applicability in parcellating the cerebellum into seven sub regions, and will explore a finer (34 object) parcellation in the future. We are currently applying MGDM to other problems such as cell segmentation and tracking, retinal layer segmentation from optical coherence tomography (OCT) images, and ultra-high resolution whole brain segmentation. We foresee MGDM providing a distinctive benefit in cell tracking/ segmentation applications, where hundreds or thousands of cells need to be segmented and tracked. Employing topology priors would prevent cells that touch from merging labels while simultaneously allowing cells that split to be tracked separately.
Source code and demonstrations
Source code and MATLAB demonstrations can be found on the MGDM NITRC page.
- Compiled MGDM code and MATLAB scripts can be downloaded from NITRC. This release also contains several demonstrations of MGDM.
- Instructions for checking out and compiling the MGDM source code.
- Users experienced with deformable models can take full advantage of MGDM by specifying boundary-specific speeds.
Publications
About MGDM
- J.A. Bogovic, J.L. Prince, and P.-L. Bazin, "A Multiple Object Geometric Deformable Model for Image Segmentation", Comput. Vis. Image Und., 117(2):145-157, 2013. (doi) (PubMed)
- X. Fan, P.-L. Bazin, J. Bogovic, Y. Bai, and J.L. Prince, "A multiple geometric deformable model framework for homeomorphic 3D medical image segmentation", IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, Alaska, June 24-26, 2008. (doi)
- X. Fan, P.-L. Bazin, and J.L. Prince, "A Multi-Compartment Segmentation Framework With Homeomorphic Level Sets.", IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, Alaska, June 24-26, 2008. (PubMed)
Using MGDM
- A. Carass, A. Lang, M. Hauser, P.A. Calabresi, H.S. Ying, and J.L. Prince, "Multiple-object geometric deformable model for segmentation of macular OCT", Biomed. Opt. Express, 5(4):1062-1074, 2014. (doi)
- J.A. Bogovic, P.L. Bazin, S.H. Ying, and J.L. Prince, "Automated Segmentation of the Cerebellar Lobules using Boundary Specific Classification and Evolution", 23rd Conference on Information Processing in Medical Imaging (IPMI 2013), Asilomar California, USA, June 29 - July 3, 2013. (doi)
- J. Stough, C. Ye, S.H. Ying, and J.L. Prince, "Thalamic Parcellation from Multi-Modal Data using Random Forest Learning", Tenth IEEE International Symposium on Biomedical Imaging (ISBI 2013), San Francisco, CA, April 7 - 11, 2013.
- C. Ye, J.A. Bogovic, S.H. Ying, and J.L. Prince, "Segmentation of the Complete Superior Cerebellar Peduncles using a Multi-object Geometric Deformable Model", Tenth IEEE International Symposium on Biomedical Imaging (ISBI 2013), San Francisco, CA, April 7 - 11, 2013.
- Z. Yang, J.A. Bogovic, A. Carass, M. Ye, P.C. Searson, and J.L. Prince, "Automatic Cell Segmentation in Fluorescence Images of Confluent Cell Monolayers Using Multi-object Geometric Deformable Model (MGDM)", Proceedings of SPIE Medical Imaging (SPIE-MI 2013), Orlando, FL, February 9-14, 2013. (doi)
- C. Ye, J.A. Bogovic, S.H. Ying, and Jerry L. Prince, "Parcellation of the thalamus using diffusion tensor images and a multi-object geometric deformable model", Proceedings of SPIE Medical Imaging (SPIE-MI 2013), Orlando, FL, February 9-14, 2013. (doi)
References
- P.-L. Bazin, L.M. Ellingsen, and D.L. Pham, "Digital homeomorphisms in deformable registration", Information Processing in Medical Imaging, 20:211-222, 2007. (PubMed)