GVF and Shape Analysis

In addition to its use as an external field for active contours, GVF appears to have interesting connections to the medial axis analysis of shape. The medial axis transform (MAT) [33] has long been used to describe both an object's shape and the relationship among an object's natural parts [34]. The MAT representation is known to be extremely sensitive to small boundary perturbations, however. To address this difficulty, Pizer et al. [35] introduced the multi-scale medial axis transform or core which incorporates a scale space into the MAT by computing the maximum medialness over scale. Medialness is a measure of how close a point is to an object's skeleton. Because core analysis operates across scales, it reduces the noise sensitivity of the MAT yet maintains almost all the desirable properties of MAT. In this section, we show that by applying a simple algebraic transformation on the magnitude of a GVF field, we get a representation strongly resembling a medialness function.

The GVF fields of Figs. 2b, 3a, 5b, and 6b reveal a common trait at the center of each of the objects. In particular, in each figure there is a single point or collection of points at which the GVF vectors go to zero. This is caused by the inherent ``competition'' in the GVF formulation, in which vectors that are ``trying'' to point toward an edge (because of the diffusion process) are balanced between edges. We further demonstrate this phenomenon by computing the GVF for the eight shapes shown in Fig. 13 and displaying their magnitudes. Inside each of these shapes, the GVF magnitude, which we denote by $\mbox{mag(GVF)} = \vert{\bf v}(x,y)\vert$, appears to diminish along the set of points comprising the classical medial axis skeleton of the shape (cf. [33]). However, it is also apparent that mag(GVF) does not necessary go to zero on this set. In particular, for the square shown in Fig. 13b, the medial axis skeleton is the set of points running diagonally between opposing corners, forming an ``X''. There is evidence of this ``X'' pattern in this figure, but mag(GVF) is clearly not zero on the ``X''.

On the other hand, each of the simpler objects in Fig. 13 appears to have a single point in its interior at which mag(GVF) is minimum -- a kind of shape origin. The more complicated shapes in Figs. 13f, g, and h violate this principle because they involve multiple parts. It seems reasonable to conjecture that local minima of mag(GVF) represent shape origins of the ``parts'' comprising a shape.

Since mag(GVF) is grayscale, not binary, we could think of it as giving a measure of how close a point is to the central axis of the shape. In this sense, mag(GVF) could be used to give a measure of ``medialness'' in the sense of cores. Since medialness is normally larger when near the shape median rather than small, two possible measures of medialness are

$$\begin{eqnarray*}{\cal M}^1(x,y) & = & \frac{1}{1 + \vert{\bf v}(x,y)\vert^q}\,,... ... {\cal M}^2(x,y) & = & e^{-\frac{\vert{\bf v}(x,y)\vert}{\tau}} \end{eqnarray*}$$

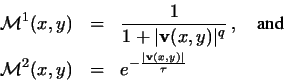
Fig. 14 shows an example of the first medialness measure applied to the ``teardrop'' shape of Fig. 13d. One can see from this figure that the medialness is larger at two other locations besides the skeleton, namely the object boundary and far outside the object. It makes sense that medialness should be larger on the boundary since the relevant shape near the boundary is the boundary itself. Also, as one moves farther away from the shape, the shape itself becomes irrelevant, and every point should be medial. Therefore, it appears that the use of mag(GVF) has very strong potential use in shape analysis using medial axis ideas and in particular to the concept of medialness in cores.