Active Contours, Deformable Models, and Gradient Vector Flow
Chenyang Xu and Jerry L. Prince
|
Overview
|
|
|
|
Introduction
|
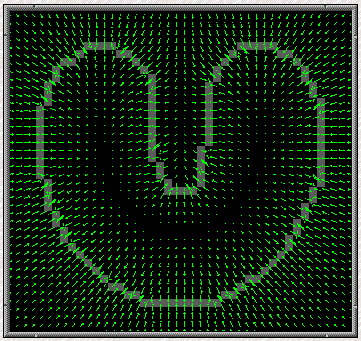
| Active contours, or snakes, are computer-generated curves that move within images to find object boundaries (note that the 3D version is often known as deformable models or active surfaces in the literature). They are often used in computer vision and image analysis to detect and locate objects, and to describe their shape. For example, a snake might be used to automatically find a manufactured part on an assembly line; one might be used to find the outline of an organ in a medical image; or one might be used to automatically identify characters on a postal letter. We have developed a new kind of snake here at the Image Analysis and Communications Laboratory. Our snake solves two key problems that have plagued the computer vision community since the introduction of snakes in 1988. These problems are that snakes cannot move toward objects that are too far away and that snakes cannot move into boundary concavities or indentations (such as the top of the character U). Previous efforts to solve these problems have not been completely successful, and have often created new problems along with the proposed solutions. |
|
Results
|
|||||||||||||||||||||||||||
|
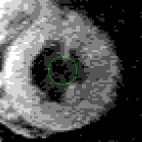
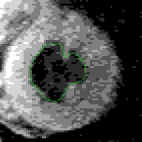
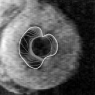
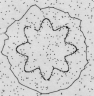
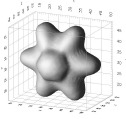
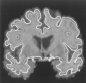
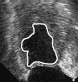
We have tested our GVF snake on many types of objects, from simple shapes to magnetic resonance images of the heart and brain. We have also extended GVF to three dimensions, where deformable surfaces, or balloons, are defined. Our ultimate research goal is to use a three-dimensional GVF balloon to find the entire human brain cortex from volumetric magnetic resonance images. The following examples demonstrate some of the properties of the GVF snake. A. Capture range and boundary concavities
B. Subjective Contours and Grayscale Images
C. Three-Dimensional GVF: Deformable Surface
|
|
Conclusion
|
|
The GVF snake is a new approach to active contours and surfaces. It focuses on the design of the external force first, and the implementation of the snake second. The computations are straightforward, i.e., the diffusion equations are simple to calculate (see publications and software below), and the result is always better than the traditional snake. As outlined in our publications, the GVF usually offers advantages over balloons and distance-based snakes as well. We anticipate and encourage widespread use of the GVF snake and the easily implemented GVF active surface as well. This new approach offers new areas for further improvement as well. For example, we have recently implemented a more general version of GVF, generalized GVF, which offers advantages when the boundary concavity is very thin. |
|
Acknowledgment
|
|
This research was supported by National Science Foundation grant MIP93-50336, CISE Directorate, Division of Microelectronic Information Processing Systems, Signal Processing Systems Program. |
|
Publications
| |||||||||||||||||||||||||||||||||
|
|
GVF FAQ (Frequently Asked Questions)
|
|
The authors get frequent emails that ask various questions regarding GVF, from general questions regarding the theory of GVF to specific questions of asking help for debugging code!. In the past, we have tried to do our best to give response to every email we receive. However, recently, both authors are occupied completely by the work and finding harder to respond to every email we receive (which is getting more and more every day). As a result, we compiled a GVF FAQ to help answer some common questions regarding the use of GVF. Therefore, we kindly ask those who send us emails read both the FAQ and GVF papers carefully before asking question in email. |
|
GVF Software
Matlab (2D Version) | ||
| ||
|
GVF for Unix, tested with Matlab version 4.2c | ||
|
GVF for Windows 95/NT, tested with Matlab version 5 | ||
|
Graphical GVF Snake Demo for Windows 95/98/NT, tested with Matlab version 5. | ||
|
C version of GVF code for Matlab (CMEX) replaces GVF.m and is significantly faster. | ||
Matlab (2D MultiGrid Version) | ||
|
2d MultiGrid implementation of Generalized Gradient Vector Flow Algorithm. |
|
Related links
|
|
|
GVF Google
Search
| ||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||
|
Science Citation Index Citations for Papers of
Interest
|
|
 Active contours, or
snakes, are computer-generated curves that move within
images to find object boundaries. Its 3D version
is often known as deformable models or active surfaces
in literature. We have developed a new kind of
snake that permits the snake to start far from the
object, and yet still draws it towards the object, and
forces it into boundary concavities. The new snake is
based on a new type of external force field, called
gradient vector flow, or GVF. This field is
computed as a spatial diffusion of the gradient of an
edge map derived from the image. This computation causes
diffuse forces to exist far from the object, and crisp
force vectors near the edges. Combining these
forces with the usual internal forces yields a powerful
computational object: the GVF snake (2D),
or the GVF deformable model (N-D).
We have experimented with GVF on line
drawings and grayscale images, including images of the
heart and brain. Several examples are shown below
and both publications and software are also available
online.
Active contours, or
snakes, are computer-generated curves that move within
images to find object boundaries. Its 3D version
is often known as deformable models or active surfaces
in literature. We have developed a new kind of
snake that permits the snake to start far from the
object, and yet still draws it towards the object, and
forces it into boundary concavities. The new snake is
based on a new type of external force field, called
gradient vector flow, or GVF. This field is
computed as a spatial diffusion of the gradient of an
edge map derived from the image. This computation causes
diffuse forces to exist far from the object, and crisp
force vectors near the edges. Combining these
forces with the usual internal forces yields a powerful
computational object: the GVF snake (2D),
or the GVF deformable model (N-D).
We have experimented with GVF on line
drawings and grayscale images, including images of the
heart and brain. Several examples are shown below
and both publications and software are also available
online.