Recursive Spatio-Temporal Function Estimation

William S. Kerwin and J.L. Prince

Overview

Interpolating or smoothing scattered data is an often encountered problem in science and engineering. When data depend on time and space, existing interpolation methods can rapidly become overwhelmed with data. In this work, we have developed a new, computationally efficient method for estimating smooth spatial functions from observations distributed over time and space. The method estimates the current spatial distribution of a function that has been observed at regular intervals in time. Potential uses include estimating the temporal changes in geophysical/ecological data, tracking the movement of a surface over time, and determining time-varying flow fields.   The method itself combines features of two well-known estimation tools: 1) kriging (a spatial interpolator) and 2) Kalman filtering (a computationally efficient recursive estimator). The stochastic models used in each of these methods are combined into a state equation representation we call the "kriging update model" that permits a recursive solution, akin to Kalman filtering, for estimating a function. The state equation representation preserves the principle assumption of kriging, that the mean is deterministic but unknown. We derive the estimate using best linear unbiased estimation, and state the result in a concise algorithm for general use in arbitrary spatial dimensions.

Problem Statement

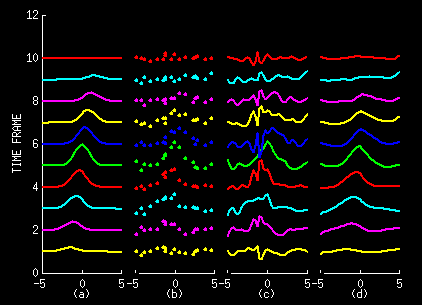
The method is best described with reference to the figure above. The far left Column (a) represents some function of both time and space z(x,t). The plot shows the function at each of ten time frames; that is z(x,t1) through z(x,t10). The second Column (b) shows observations of the function at each of the ten time frames. Random noise has been added to the samples to simulate an imperfect observation process. Our goal is to estimate the sequence of functions in Column a given the observations in Column b. This goal poses two challenges: to reject observation noise and to interpolate between observation locations.

Past Work

One possible solution is to individually apply a spatial interpolator such as kriging to the observations made at each time. Kriging models a function as z(x) = u(x) + m(x), where u(x) is a zero-mean random component and m(x) is an unknown, deterministic mean function. The function estimate is determined using best linear unbiased estimation (BLUE). Column c above shows the results of applying kriging to the data in Column b. This approach does not prove satisfactory. One of the principle drawbacks is that it does not take advantage of the slow temporal variation of the function. At the second time frame, we also have data from the first time frame; at the third time frame, we also have data from the first two time frames and so on. The method should use this past data and the temporal smoothness to produce a better estimate. While there exist extensions of kriging that do this (space-time kriging and cokriging), they run into a new challenge. As the number of time frames grows, the number of past observations becomes too large to handle practically.

Our Method

To overcome this growing data problem we have proposed a new update model for the data in which z(x,tn) = z(x,tn-1) + u(x,tn) + m(x,tn). The update components u(x,tn) and m(x,tn) are a zero-mean, stochastic portion and an unknown, deterministic mean, respectively, as in kriging. Hence, we call this model the kriging update model. Based on this data model we have derived a method for computing the best linear unbiased estimate of the function. The method is recursive so that the current estimate is simply an update of the previous estimate. Computing the estimate at each time frame involves no more computation than individually kriging the functions. However, the estimates include information from all past time frames in addition to the present one. The resulting improvement is shown in Column d above, showing the results of our algorithm applied to the data in Column b.

Discussion

This example is a simple one-dimensional one. The algorithm actually works in spaces of any dimension. Details of the method, the model and a statement of the algorithm may be found in the publications listed below. The paper also discusses an application in medical imaging.

Publications

W.S. Kerwin and J.L. Prince, "The Kriging Update Model and Recursive Time-Space Function Estimation," IEEE Transactions on Signal Processing, 47(11):2942-2952, November 1999. W.S. Kerwin and J.L. Prince, "The Kriging Update Model and Recursive Time-Space Function Estimation," JHU Tech Rep ECE 98-11, 28 pages, October, 1998. W.S. Kerwin and J.L. Prince, ``Recursive Filtering and Interpolation Algorithm for Function Sequences of Any Dimension,'' Proc. Image and Multidimensional Digital Signal Processing (IMDSP) Workshop, Alpbach, Austria. July, 1998, pp. 239-242.