

Next: Gradient Vector Flow (GVF)
Up: Gradient Vector Flow Field
Previous: Gradient Vector Flow Field
We begin by defining a non-negative edge map f(x,y) derived from the
image I(x,y) having the property that it is larger near the image
edges. Accordingly, we can use
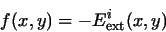 |
(9) |
where i = 1, 2, 3, or 4.
The field 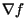 has vectors pointing toward the edges, but
it has a narrow capture range, in general. Furthermore, in homogeneous
regions, I(x,y) is constant,
has vectors pointing toward the edges, but
it has a narrow capture range, in general. Furthermore, in homogeneous
regions, I(x,y) is constant, 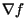 is zero, and therefore
no information about nearby or distant edges is available.
is zero, and therefore
no information about nearby or distant edges is available.
We note that other features besides edges can be sought by redefining
f(x,y) to be larger at desired features of interest, rather than
edges.
Chenyang Xu
1999-11-06