Gradient Vector Flow (GVF)

We define the gradient vector flow (GVF) field to be the vector field ${\bf v}(x,y) = (u(x,y),v(x,y))$ that minimizes the energy functional

$$\mathcal{E} = \int\!\!\int\mu({u_x}^2 + {u_y}^2 + {v_x}^2 + {v_y}^2) + \vert\nabla f\vert^2\vert{\bf v}-\nabla f\vert^2 dxdy$$ (10)

This variational formulation follows a standard principle, that of making the result smooth when there is no data. In particular, we see that when $\nabla f$ is zero, the energy is dominated by partial derivatives of the vector field, yielding a smooth field. On the other hand, when $\nabla f$ is large, the second term dominates the integrand, and is minimized by setting ${\bf v}= \nabla f$. The parameter $\mu$ is a regularization parameter governing the tradeoff between the first term and the second term. This parameter should be set according to the amount of noise present in the image (more noise, increase $\mu$).

We note that the smoothing term -- the first term within the integrand of (10) -- is the same term used by Horn and Schunk in their classical formulation of optical flow [27]. On one hand, it is known that this term leads to the Laplacian operator in the corresponding Euler equations. On the other hand, it has recently been shown that this term corresponds to an equal penalty on the divergence and curl of the vector field [28]. Therefore, the external field resulting from this minimization can be expected to be neither entirely irrotational (as are the usual snake potential fields) nor entirely solenoidal.

Using the calculus of variations [29], it can be shown that the GVF can be found by solving the following Euler equations 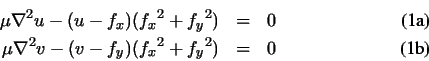  where $\nabla^2$ is the Laplacian operator. These equations give us another intuition behind the GVF formulation. We note that in homogeneous regions, the right hand side of both equations (11a) and (11b) is zero (because the gradient of f(x,y) is zero). Therefore, within these regions, u and v are each determined by Laplace's equation. This results in a type of ``filling-in'' of information taken from the boundaries of the region.