Vector Tomography

Jerry L. Prince

Overview

Vector tomography is the reconstruction of vector fields - e.g., the velocity of fluid flow or the displacement of a deformed object - from projections of components of the field. Here, we consider the following general projection measurement

(1)

which we call the inner product measurement or probe transform of the vector field . The effect of probe is to convert the vector field into a scalar by taking a point-by-point inner product. The resultant scalar field is then integrated over planes as in the 3-D Radon transform. This transformation generalizes a type of measurement equation that has been studied in 2-D and almost exclusively in the context of acoustic flow imaging using time-of-flight measurements - e.g., ultrasonic imaging in medicine, flow imaging in nondestructive evaluation, and ocean acoustic tomography.

The use of inner product measurements has several potential advantages in the imaging of vector fields. First, forming the inner product has the effect of performing a derivative on the measured data, normally the first step in numerical inversion. Thus, the measurement process itself performs an operation which is normally prone to numerical instability. Second, if a field is known to be either irrotational or solenoidal, then fewer measurements than are required to recover a general vector field may be used to recover just that component alone. This saves measurements and potentially reduces the effects of noise. Finally, some properties of the field, such as vorticity, can be calculated from a single component of the field. Thus, if such a property is desired, it may be found from a smaller number of measurements than would be required to reconstruct the full vector field.

Theory

According to Helmholtz's Theorem, a vector field with homogeneous boundary conditions can be uniquely written as where . The scalar function is called the scalar potential and the vector function is called the vector potential. The irrotational component satisfies while the solenoidal component satisfies .

Assuming that the probe only depends on orientation, leads to the following projection theorem

which is a projection theorem relating the probe transform directly to the potential functions. This theorem is the starting point for deriving the following convolution backprojection reconstruction formulas.

It follows from the projection theorem that the components and can be imaged separately. In particular, if then since the solenoidal component of the field is invisible. The following formula can be established

where the double subscript indicates second derivative with respect to and is the unit hemisphere.

In a similar fashion, we see from the projection theorem that the irrotational part of the field is invisible if is orthogonal to . Since the linear subspace orthogonal to is two-dimensional, two probes and can be selected which are linearly independent and orthogonal to . If form a right-handed orthonormal basis, then

Simulations

Three vector fields were defined on the unit cube and sampled on a 16x16x16 lattice. The first field is irrotational, the second is solenoidal, and the third is the sum of these two. The scalar and vector potentials

where are used to define the irrotational and solenoidal fields

Assigning and gives a third vector field which has both irrotational and solenoidal components. Also, it is readily verified that , , and .

The original and reconstructed fields appear in the following figure.

	Original	Reconstruction
Scalar Potential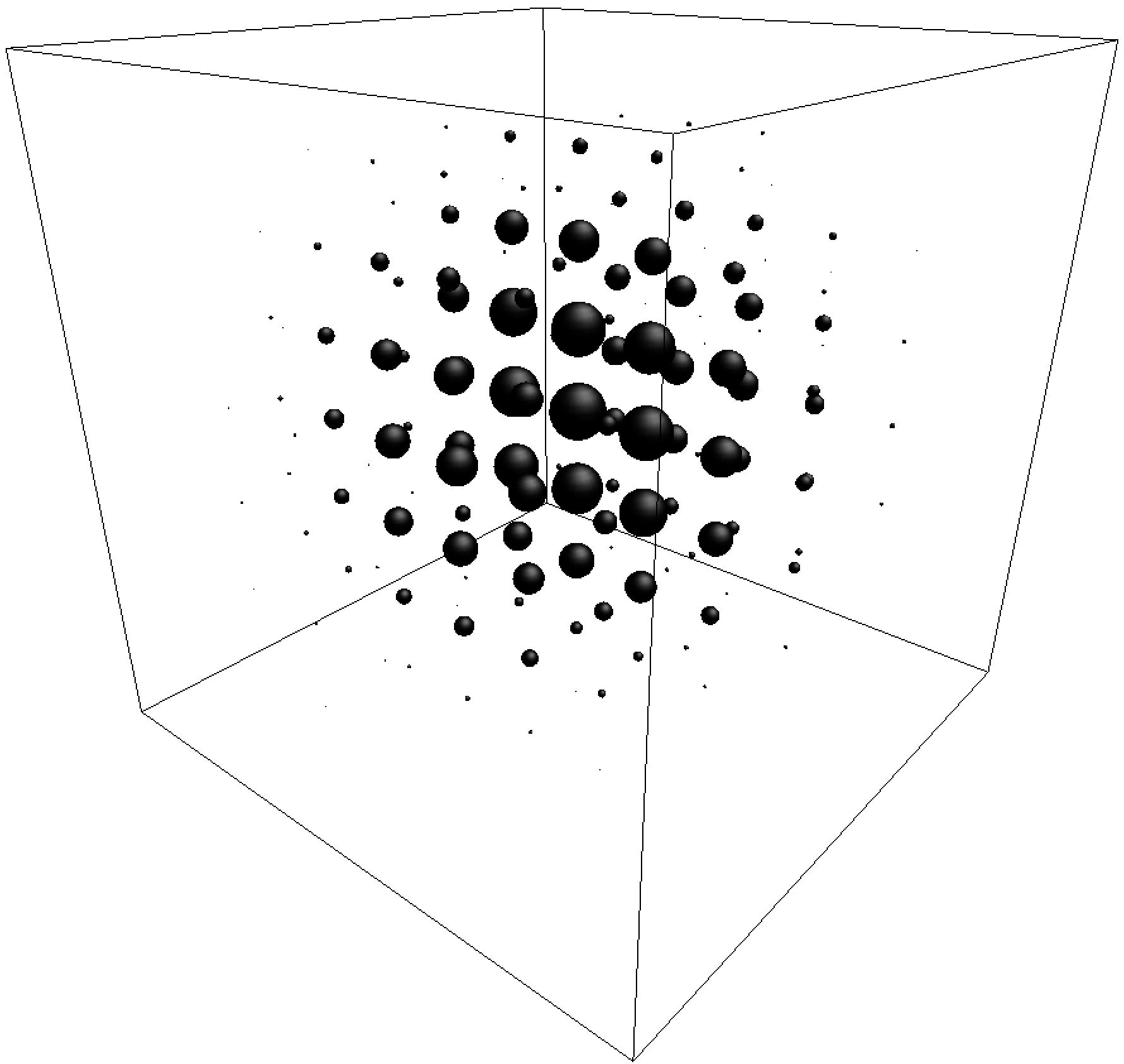
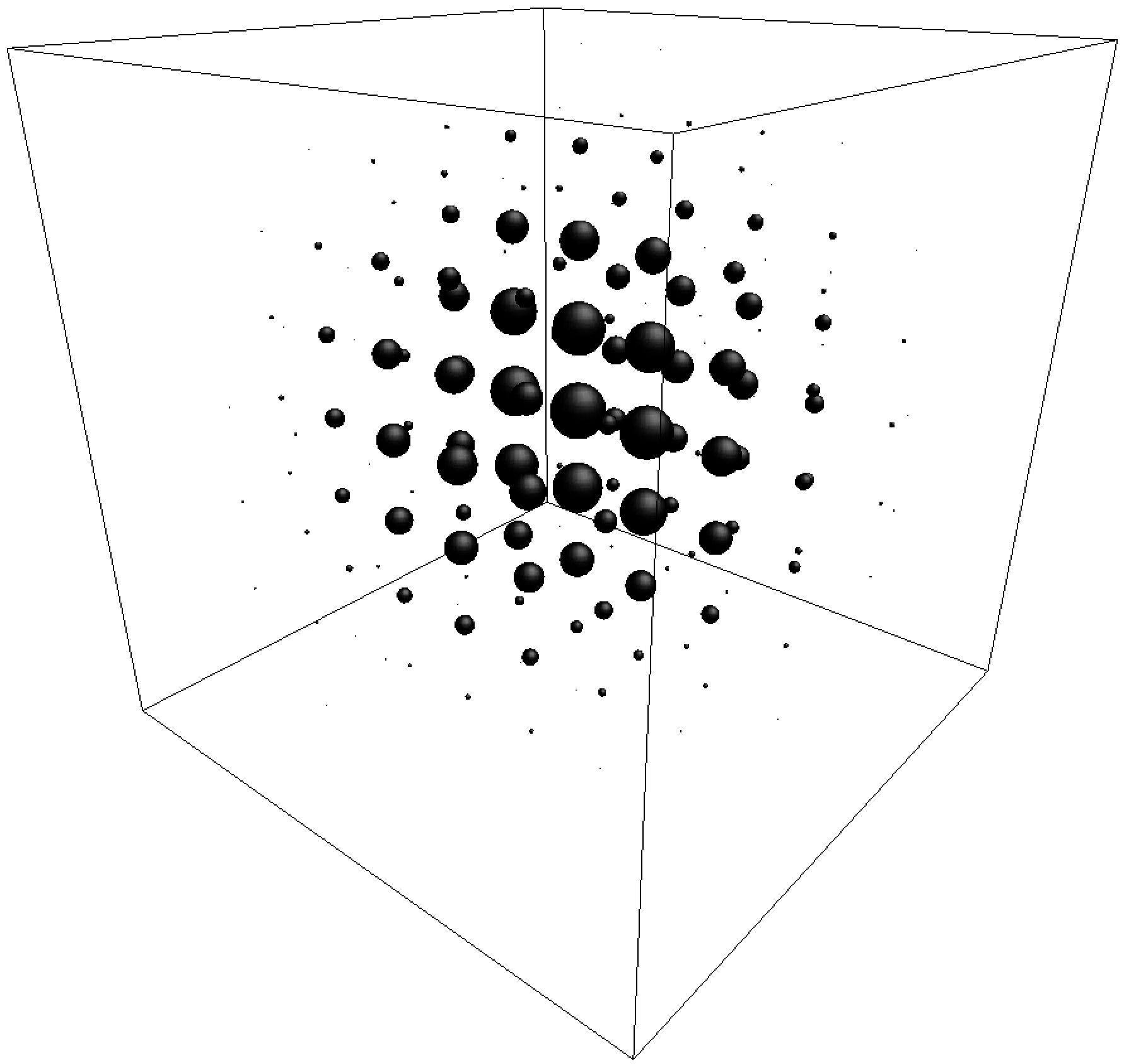Vector Potential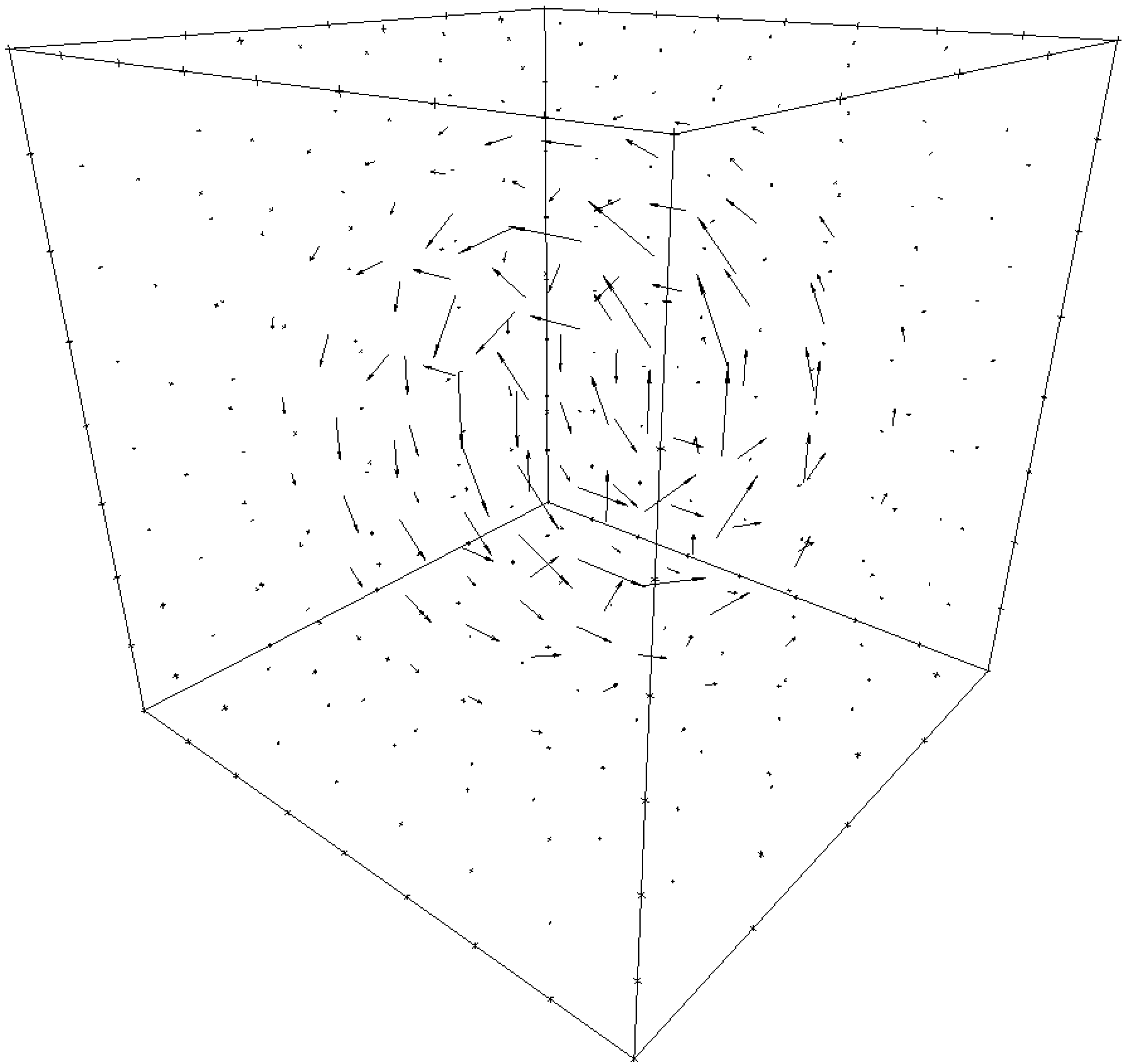
Irrotational Part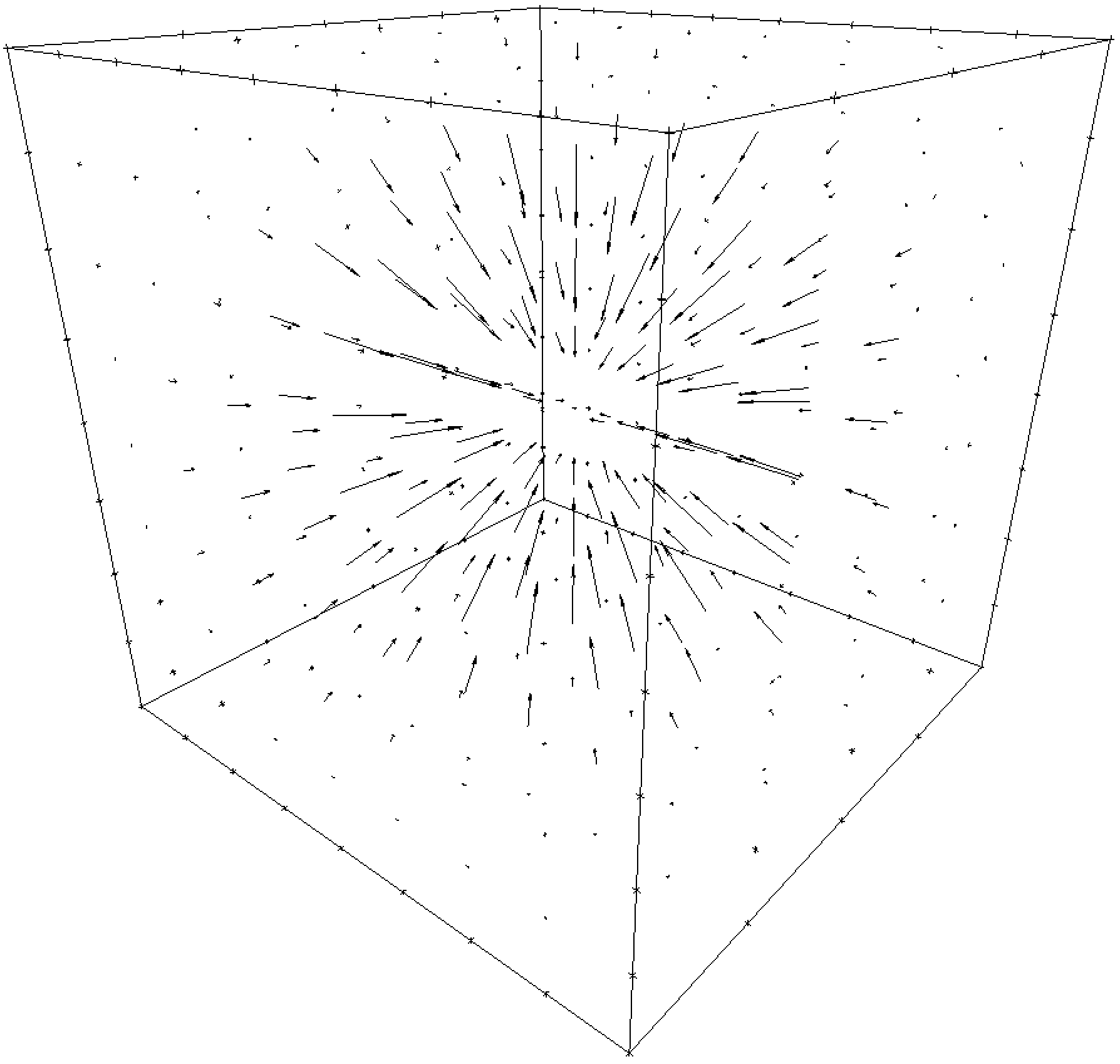
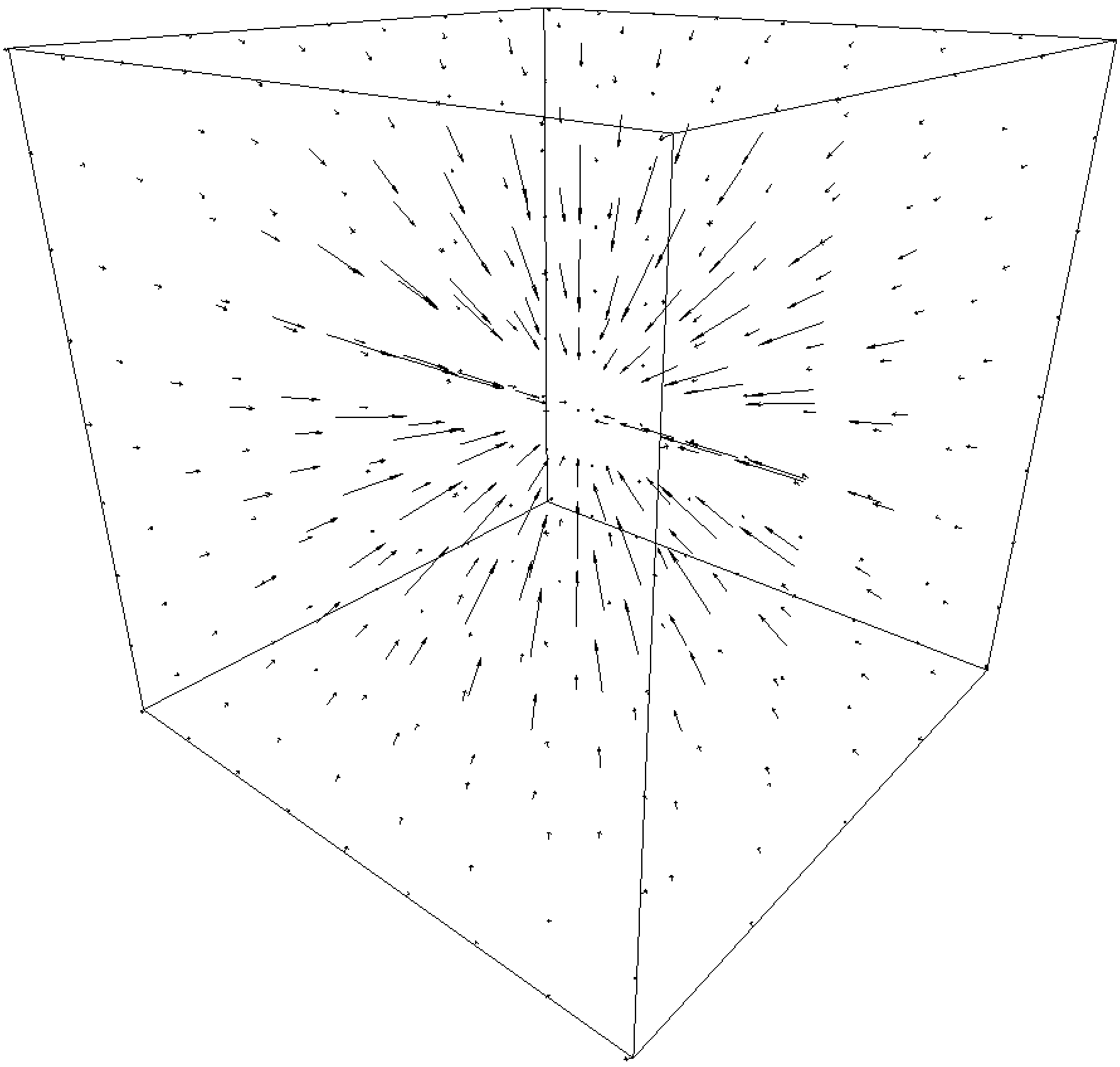Solenoidal Part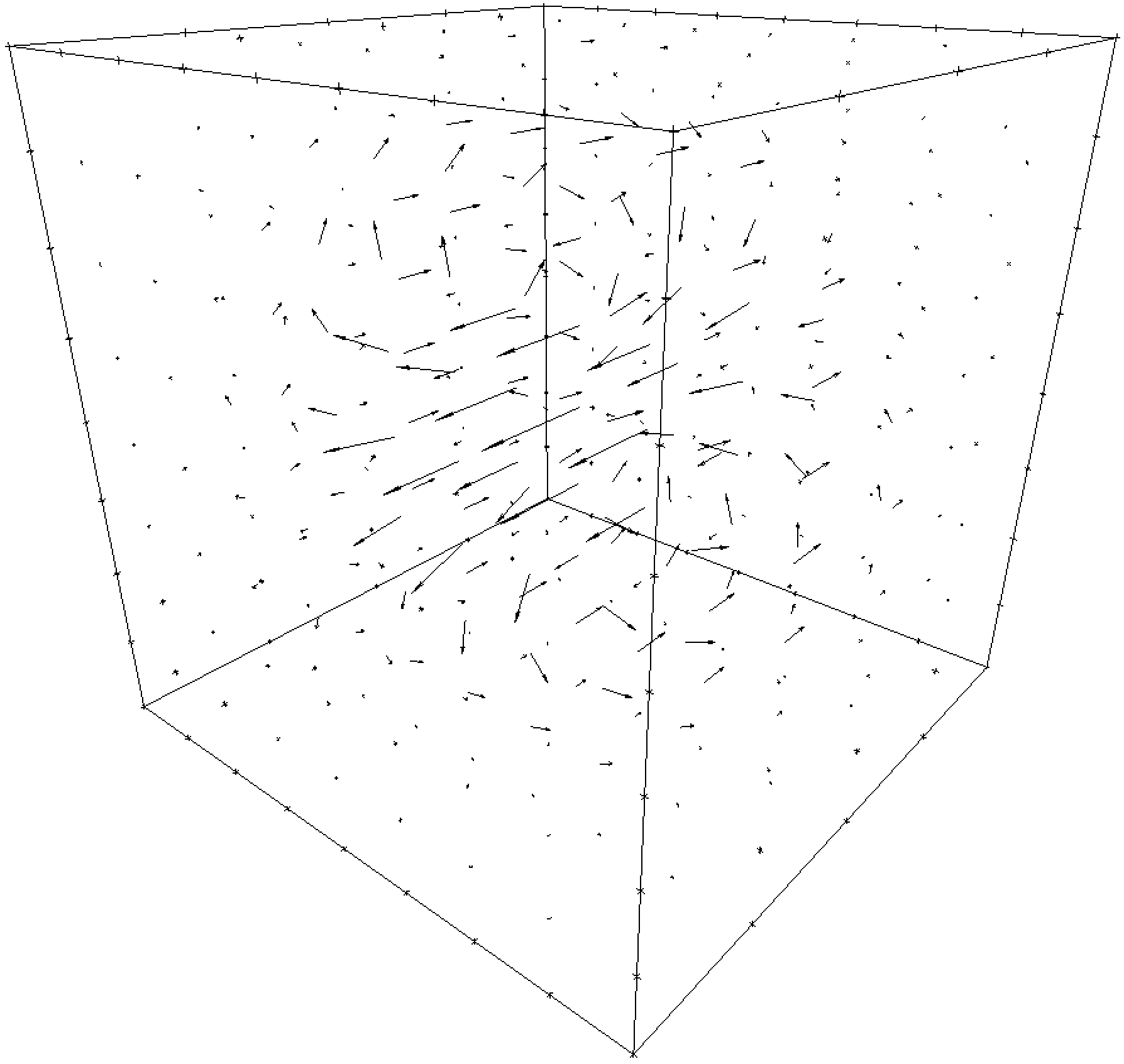
Whole Field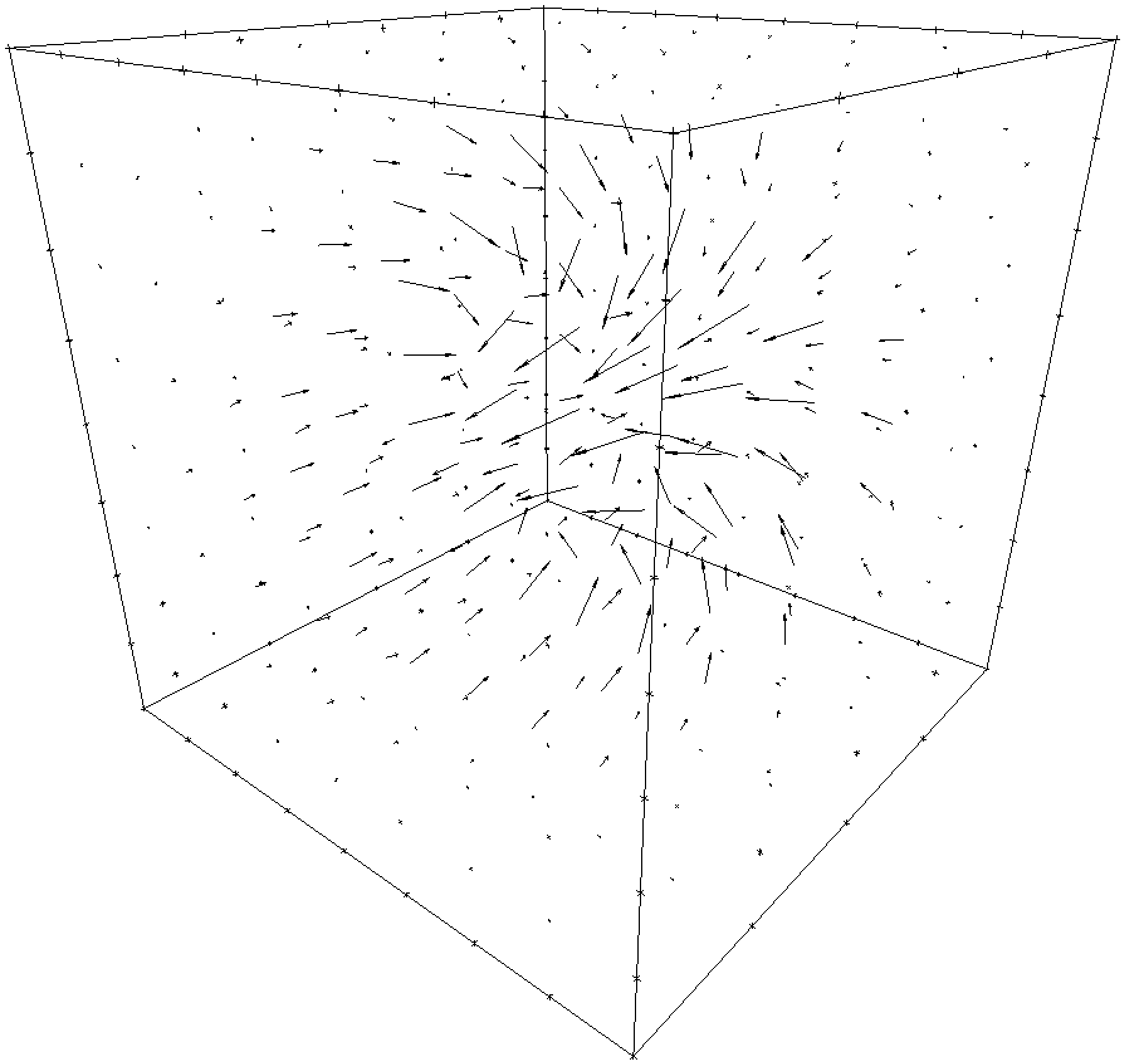

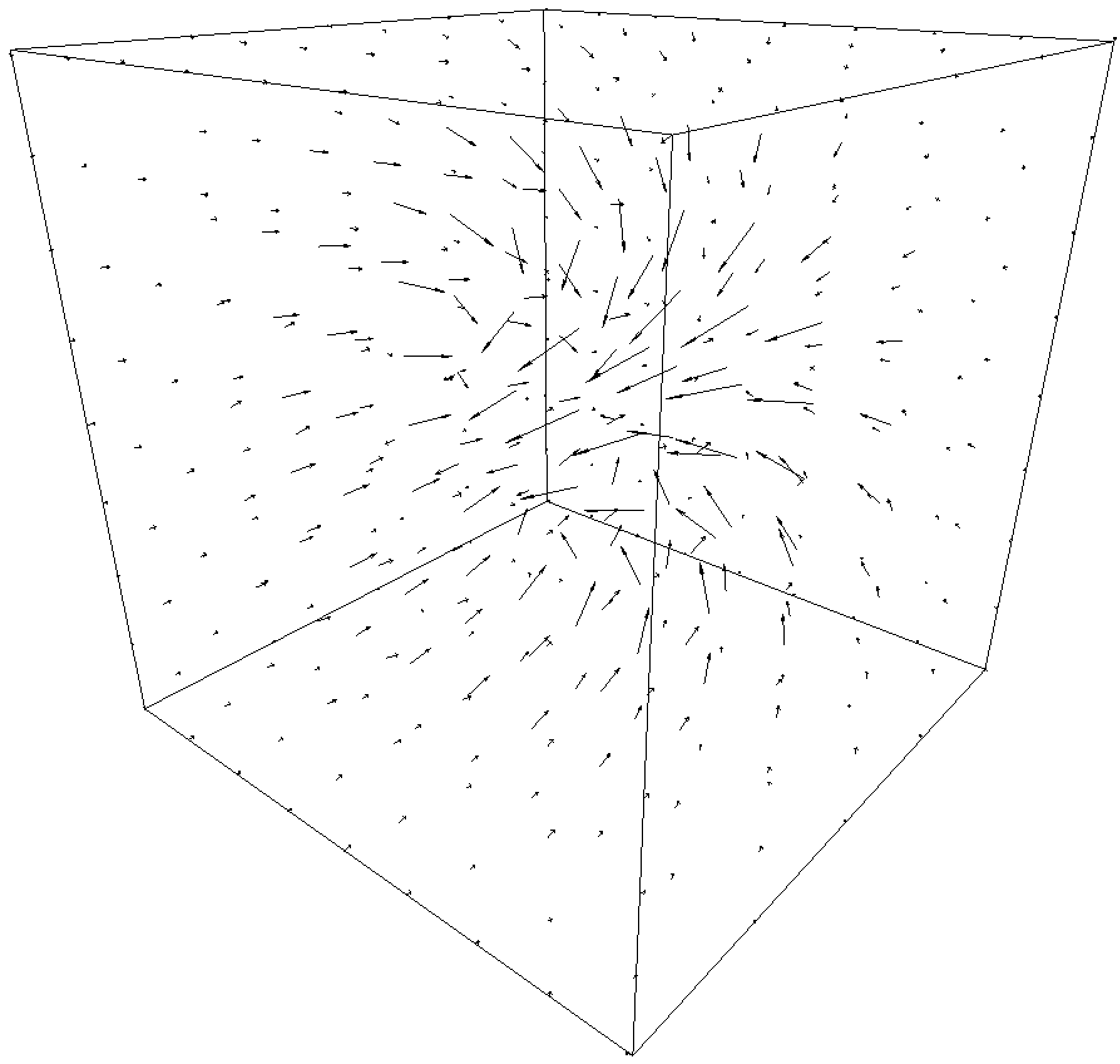Conclusion

This work provides a basic analogy between vector tomography and standard computed tomography through a projection theorem and convolution backprojection reconstruction formulas. In publications provided below, additional projection theorems and reconstruction formulas are provided, boundary conditions are addressed, and connections between vector tomography and magnetic resonance imaging are provided. Although the framework presented here used probes that form a right-handed frame, linear independence is all that is required, and field components can be reconstructed from fewer than three probes. These properties may allow the use of the probe transform formalism in new applications. Finally, the approach used to generate simulations in this work - i.e., synthetically scanning a discrete vector field and reconstructing the potentials or field components - represents (as far as we know) a completely new way to extract both potential functions and field components from a sampled vector field.

Publications

1. J. L. Prince, "Tomographic Reconstruction for 3-D Vector Fields," Proceedings of ICAASP93, IEEE #93CH3252-4, April 1993.
2. J. L. Prince, "Tomographic Reconstruction of 3-D Vector Fields Using Inner Product Probes," IEEE Transactions on Image Processing, vol. 3. no. 2, pp. 216-219, March 1994.
3. J. L. Prince, "A Convolution Backprojection Formula for Three-Dimensional Vector Tomography," Proceedings of the 1994 IEEE Int'l Conf. on Image Processing, vol. 2, pp. 820-824, November 1994.
4. J. L. Prince, "Tomographic Imaging of Vector Fields," Invited Paper, OSA Spring Topical Meetings, Signal Recovery and Synthesis V, pp. 2-4, March 12-17, 1995
5. J. L. Prince, "Convolution Backprojection Formulas for 3-D Vector Tomography with Application to MRI," IEEE Transactions on Image Processing, vol. 5, no. 10, pp. 1462-1472, October 1996.
6. N. F. Osman and J. L. Prince, "Reconstructed Potential Functions in Bounded Domain Vector Tomography," Proc. Conf. Inf. Sci. Sys., The Johns Hopkins Univ., pp. 891-895, March 19-21, 1997.
7. N. F. Osman and J. L. Prince, "Reconstruction of Vector Fields in Bounded Domain Vector Tomography," Proceedings of ICIP97, vol. 1, pp.476-479, Santa Barbara CA, Oct. 26-29, 1997.
8. N. Osman and J. L. Prince, "3-D Vector Tomography on Bounded Domains," Inverse Problems, vol. 14, pp. 185-196, 1998.