From IACL
Jump to: navigation, search

Watershed Segmentation of the Human Brain Cortex

Maryam E. Rettmann, Xiao Han, Chenyang Xu, and Jerry L. Prince





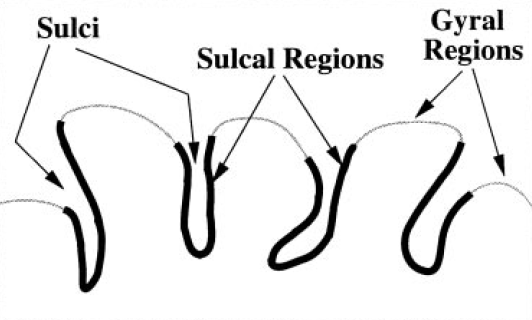
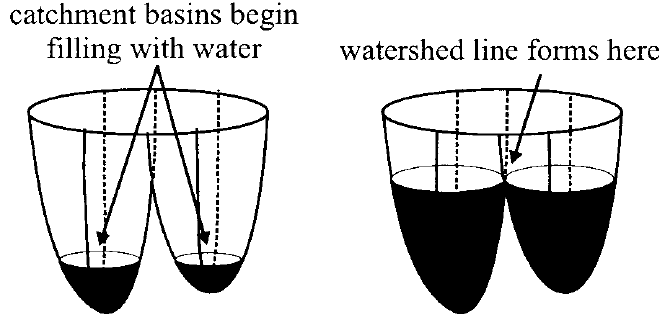
Overview: The human cortical surface is a highly complex, folded structure. Sulci, the spaces between the folds, define location on the cortex and provide a parcellation into anatomically distinct areas. A topic that has recently received increased attention is the segmentation of these sulci from magnetic resonance images, with most work focusing on extracting either the sulcal spaces between the folds or curve representations of sulci. Unlike these methods, we propose a technique that extracts actual regions of the cortical surface that surround sulci, which we call "sulcal regions." The method is based on a watershed algorithm applied to a geodesic depth measure on the cortical surface. A well-known problem with the watershed algorithm is a tendency toward over segmentation, meaning that a single region is segmented as several pieces. To address this problem, we propose a post processing algorithm that merges appropriate segments from the watershed algorithm. The sulcal regions are then manually labeled by simply selecting the appropriate regions with a mouse click and a preliminary study of sulcal depth is reported. Finally, a scheme is presented for computing a complete parcellation of the cortical surface.

Introduction: Quantitative anatomic studies of the human cortex are challenging due to its highly complex, convoluted folding pattern. The various folds, called gyri, and the spaces between the folds, called sulci, define location on the cortex and provide a parcellation of the cortex into anatomically distinct areas. With the advancement of magnetic resonance (MR) imaging techniques, high-resolution, high-contrast three-dimensional images of the brain can now be routinely acquired in vivo. As a result, methods for modeling the cortical surface from these images have emerged, providing a means for furthering the understanding of morphometric variability in human populations. A topic that has recently received increased attention is the study of sulci, in particular, their segmentation from MR images.


Previous work in the segmentation of sulci has focused on fitting a surface, finding a set of points, or extracting volumetric regions within sulcal spaces. Other work has focused on extracting curve representations of the sulci. Unlike these methods, we propose a technique that segments the actual cortical regions surrounding sulci. The advantage of segmenting actual cortical regions is that it allows for a direct geometric study of the cortical surface and provides a means for mapping functional activation sites. For ease of terminology, we refer to our segmented regions as sulcal regions, which define the buried regions of cortex surrounding the sulcal spaces. Another advantage of the proposed method is that it segments sulcal regions on the medial surface as well as the lateral and inferior surfaces. In addition, this segmentation method is completely automated and can be used as a visualization tool for manual labeling of individual sulcal regions.



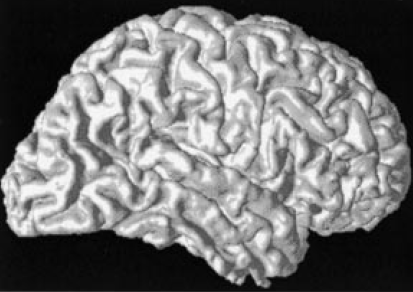
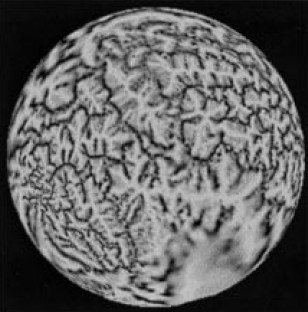
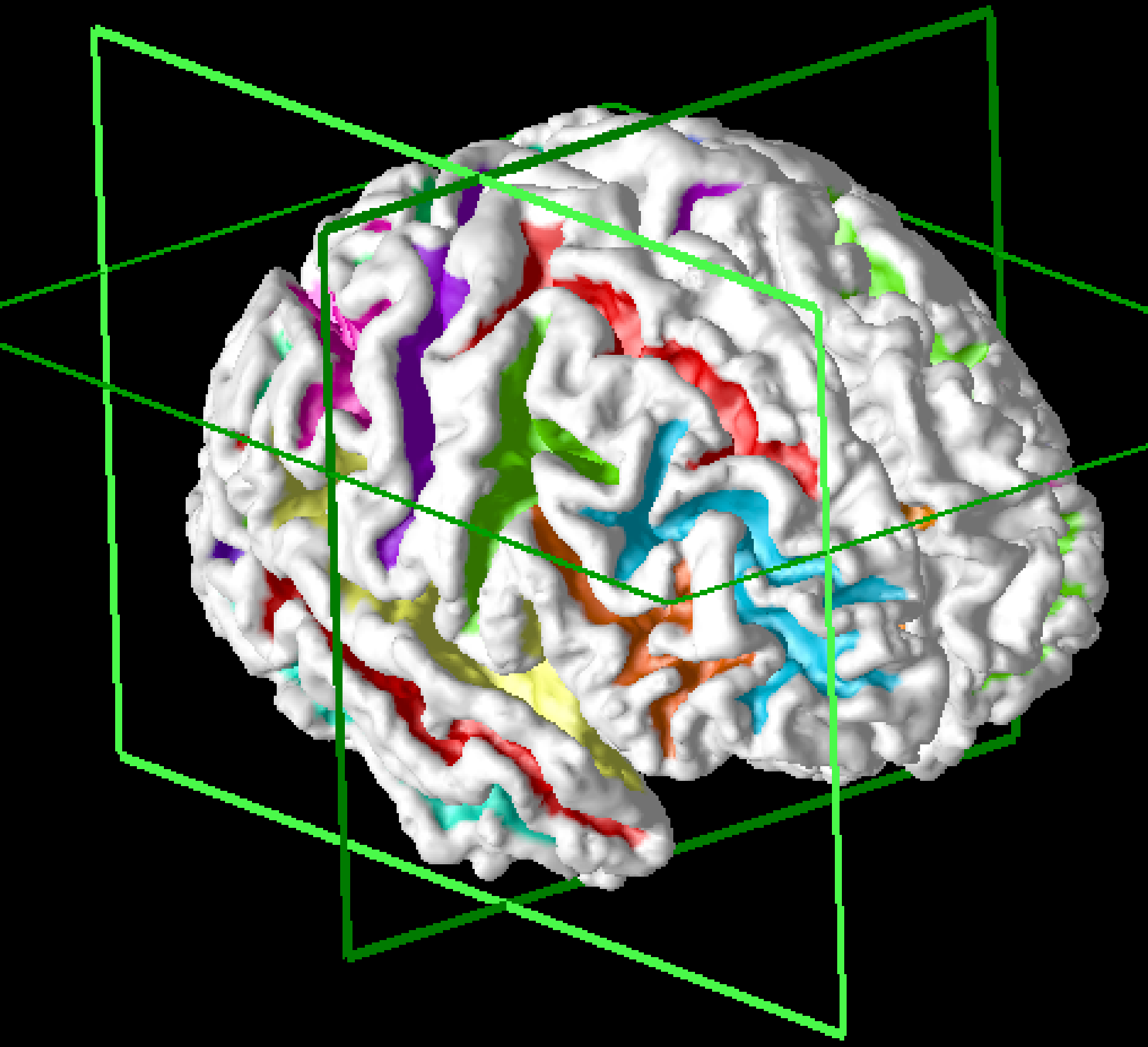
Method: A cortical surface is extracted from volumetric MR data using CRUISE and the surface is mapped to the sphere for computational and visualization purposes. A typical surface and its spherical map (displaying mean curvature) is shown below.

Sulcal regions are "buried cortices" as shown below
Watershed segmentation proceeds by computationally immersing the underside of the cortex into a water bath as illustrated below
To accomplish this, the hemispheres are first separated and then a deformable surface "shrinkwrap" algorithm is run on each hemisphere, thereby defining the outer surface of each hemisphere. All nodes of the triangle mesh representing a cortex that are touching the shrinkwrap surface are deemed to be "gyral regions." Two distance maps are computed: a 3D Euclidean map and a geodesic distance map. The geodesic map is computed using a fast marching algorithm run on the triangle mesh. All nodes greater (Euclidean distance) from the gyral regions are considered to be sulcal regions. A Euclidean distance map and a sulcal segmentation are shown below:
A geodesic map is shown below:
A 2D watershed algorithm is then run on the sulcal regions that were previously segmented, yielding finer regions, as shown below:
This result is an "over segmentation" - very typical of watershed algorithms - and therefore a merging of catchment basins operation is done, yielding the result below:



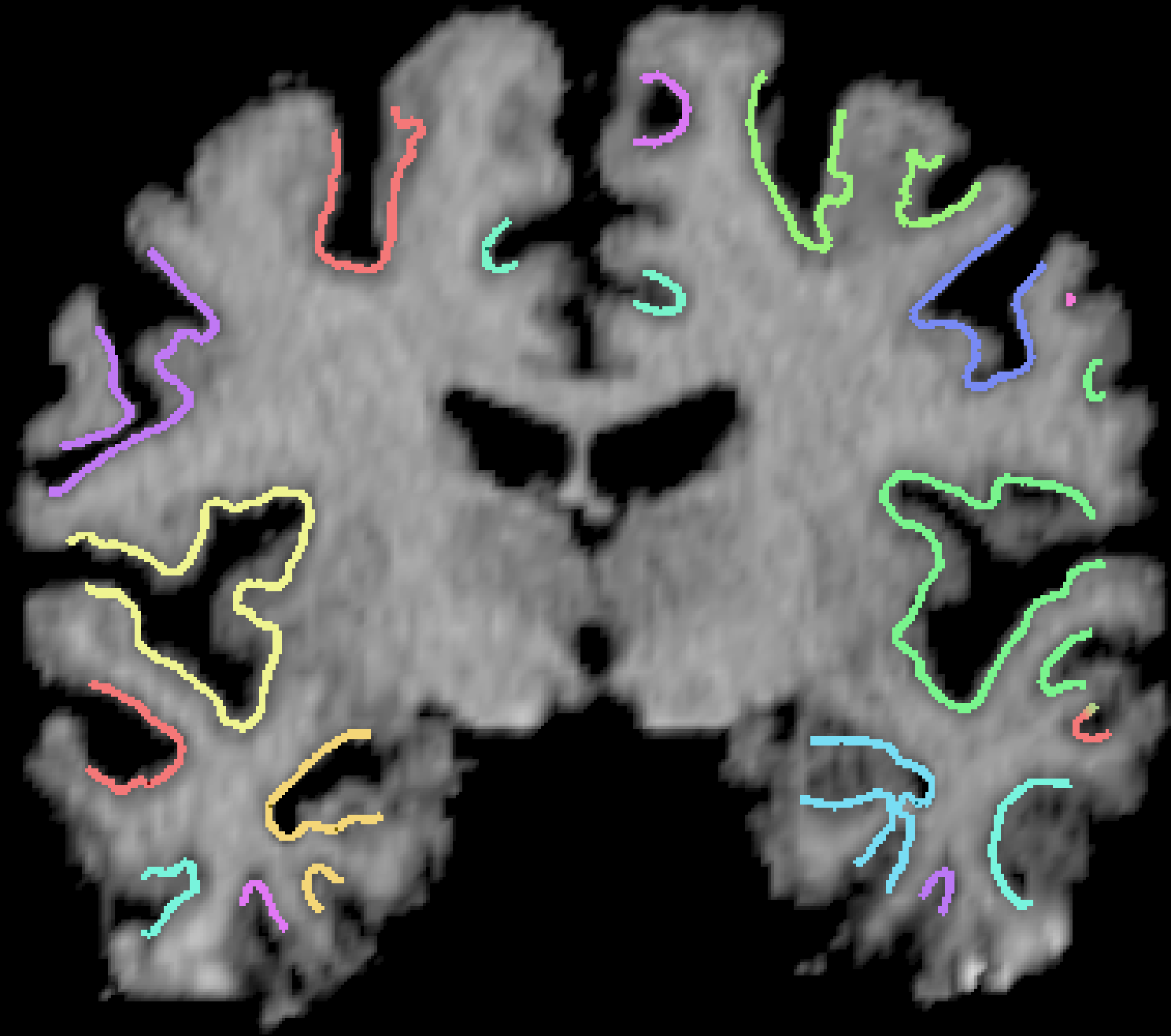
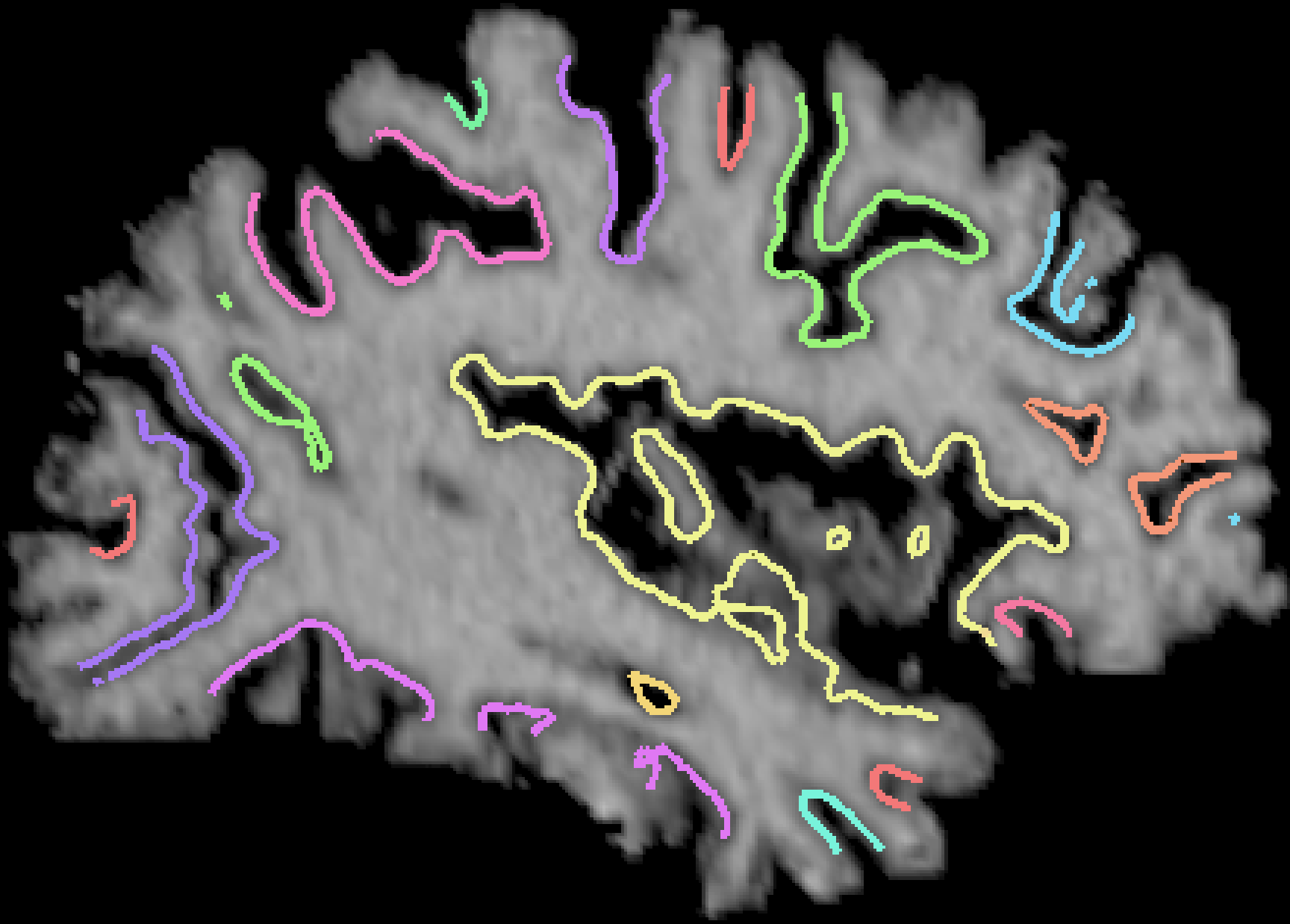
Results: Over 1,000 brains have been processed using this algorithm, which is fully automatic. A typical result is shown in cross sections below:

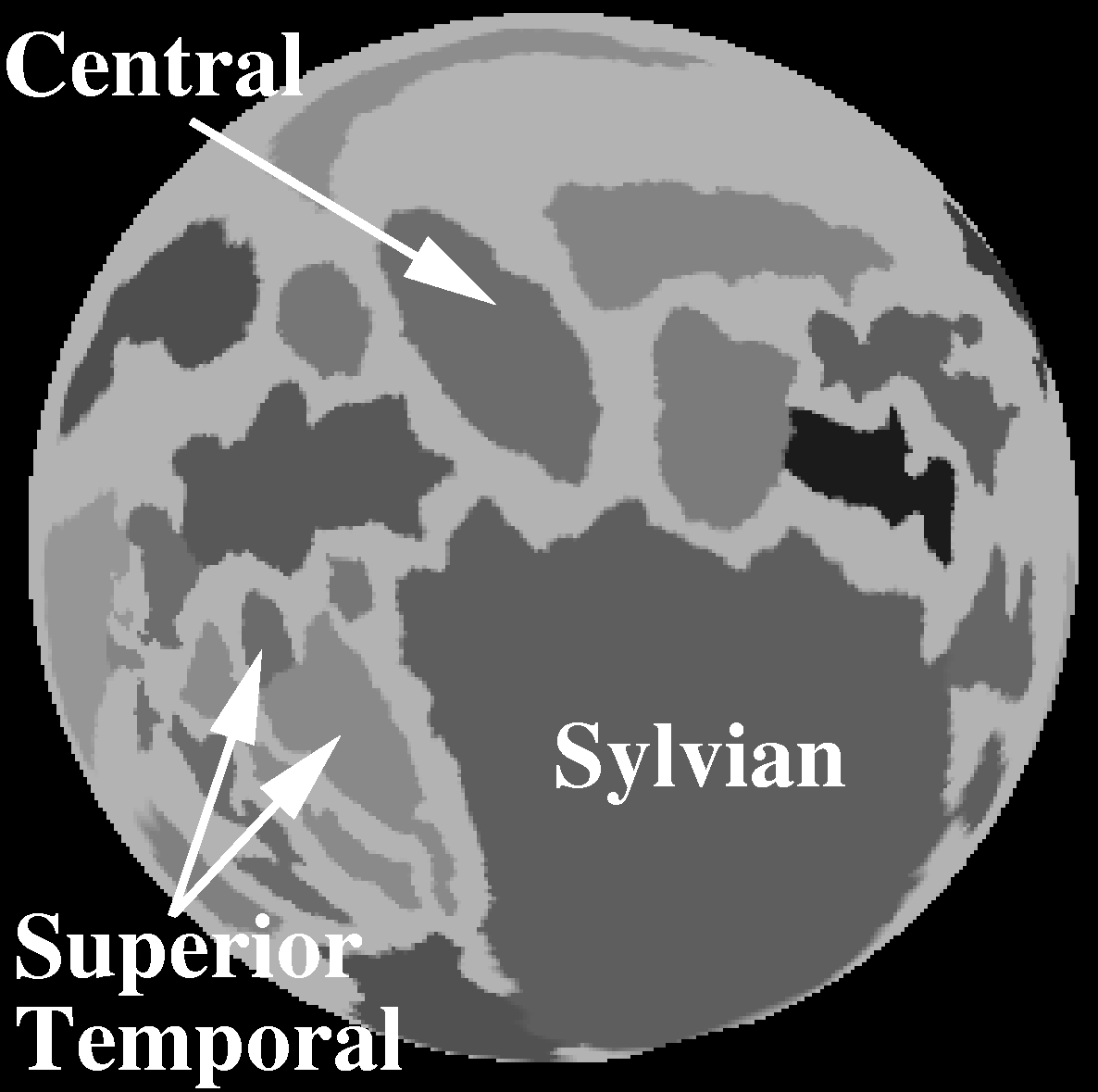
A measure of average geodesic depth in the Central, Sylvian, and Superior Temporal Sulci was computed for 15 subjects, and is given below:

Geodesic Depth in Milimeters (N = 15)

SulcusMeanSDMaxMin
Ce (L)20.52.2724.516.1
Ce (R)20.11.2022.018.1
Syl (L)40.82.7145.036.7
Syl (R)39.32.8946.235.7
ST (L)19.11.5722.116.4
ST (R)21.22.6425.616.0

Conclusion: Watershed segmentation of sulcal regions can be used for automatic identification of sulcal regions in the analysis of changes due to aging and disease or for the automatic generation of cortical landmarks for applications such as intersubject registration. These methods have been used to analyze changes in cortical thickness and shape in (Rettmann et al., 2006).


Publications

  1. M. E. Rettmann, C. Xu, D. L. Pham, D. N. Yu, and J. L. Prince, "On Automated Segmentation of Buried Gyri," 5th International Conference on Functional Mapping of the Human Brain, June 1999. NeuroImage, vol. 9, no. 6, pg. 143, 1999.
  2. M. E. Rettmann, C. Xu, D. L. Pham, and J. L. Prince, "Automated Segmentation of Sulcal Regions", Second International Conference on Medical Image Computing and Computer Assisted Interventions (MICCAI'99), pp. 158-167, September 1999.
  3. X. Han, M. E. Rettmann, C. Xu, and J. L. Prince, "Morphology on Triangle Meshes Using Geodesic Distance," Conf. on Info. Sci. Sys., Princeton University March 15-17, 2000.
  4. M. E. Rettmann, X. Han, D. L. Pham, J. L. Prince, "Geodesics for Sulcal Segmentation and Depth Measurements," NeuroImage Human Brain Mapping 2000 Meeting, Poster No. 667, NeuroImage Vol. 11, No. 5, May 2000.
  5. M. E. Rettmann, X. Han, and J. L. Prince, "Watersheds on the cortical surface for automated sulcal segmentation," Proceedings IEEE Workshop on Mathematical Methods in Biomedical Image Analysis, Hilton Head Island, SC, Jun 11-12, p.20-27, June 2000.
  6. X. Han, M. E. Rettmann, C. Xu, and J. L. Prince, "Automatic segmentation editing for cortical surface reconstruction," Proc. SPIE Medical Imaging, Conf. 4322, Paper 22, San Diego, February 2001.
  7. M. E. Rettmann, X. Han, J. L. Prince, "Automated Parcellation of the Cortical Surface for Computation of Regional Gyrification Indices," Abstract 230, Human Brain Mapping, Brighton UK, 2001.
  8. X. Tao, X. Han, M.E. Rettmann, J. L. Prince, and C. A. Davatzikos, "Statistical Study on Cortical Sulci of Human Brains," Information Processing in Medical Imaging, 17th Int'l Conference, Davis CA, pp.475-487, June 2001.
  9. M. E. Rettman, X. Han, and J. L. Prince, "Automated Sulcal Segmentation Using Watersheds on the Cortical Surface," NeuroImage, vol. 15, no. 2, pp. 329-344, February 1, 2002
  10. M.E. Rettmann, X. Tao, J. L. Prince, "Assisted labeling techniques for the human brain cortex," Proc. SPIE Medical Imaging 2002, vol. 4684, pp. 179-190, San Diego, CA, Feb. 23-28, 2002.
  11. K. Behnke, M. Rettmann, D. Pham, D. Shen, S. Resnick, C. Davatzikos, and J. L. Prince, "Automatic classification of sulcal regions of the human brain cortex using pattern recognition," in Proc. SPIE's Medical Imaging, San Diego, CA, Feb. 15-20, 2003.
  12. M. E. Rettmann, J. L. Prince, and S. M. Resnick. "Analysis of Sulcal Shape Changes Associated with Aging," in Proc. Human Brain Mapping, New York, NY, June 18-22, 2003.
  13. D. Tosun, M. E. Rettmann, and J. L. Prince, "Mapping Techniques for Aligning Sulci Across Multiple Brains," Conference on Medical Image Computing and Computer Assisted Intervention, Montreal, 14-18 November 2003.
  14. D. Tosun, M.E. Rettmann, and J. L. Prince, "Mapping Techniques for Aligning Sulci Across Multiple Brains," Medical Image Analysis, vol.8, pp. 295-309, 2004.
  15. D. Tosun, M. E. Rettmann, X. Han, X. Tao, C. Xu, S. M. Resnick, D. Pham, and J. L. Prince, "Cortical Surface Segmentation and Mapping," NeuroImage, vol. 23, pp. S108-S118, 2004.
  16. X. Han, D.L. Pham, D. Tosun, M.E. Rettmann, C. Xu, and J. L. Prince, "CRUISE: Cortical Reconstruction Using Implicit Surface Evolution," NeuroImage, vol. 23, pp. 997-1012, 2004.
  17. M.E. Rettmann, D. Tosun, X. Tao, S.M. Resnick, and J.L. Prince, "Program for the Assisted Labeling of Sulcal Regions (PALS): Description and Reliability," NeuroImage, volume 24, issue 2, pp. 398-416, 15 January 2005.
  18. M.E. Rettmann, D. Tosun , X. Tao, S.M. Resnick, and J.L. Prince, "Mapping Cross-Sectional Differences in Cortical Thickness During Aging," 11th Annual Meeting of the Organization for Human Brain Mapping (HBM), Toronto, Ontario, Canada, June 12-16, 2005.
  19. M. E. Rettmann, M. A. Kraut, J. L. Prince, and S. M. Resnick, "Cross-Sectional and Longitudinal Analyses of Anatomical Sulcal Changes Associated with Aging," Cerebral Cortex, 16:1584-1594, November 2006.



Retrieved from "http://midiron.iacl.net/index.php?title=Research&oldid=15703"