Difference between revisions of "Automatic magnetic resonance spinal cord segmentation"
m |
|||
| (16 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <meta name="title" content="Automatic magnetic resonance spinal cord segmentation"/> | + | <!-- <meta name="title" content="Automatic magnetic resonance spinal cord segmentation"/> --> |
{{h2|Automatic magnetic resonance spinal cord segmentation}} | {{h2|Automatic magnetic resonance spinal cord segmentation}} | ||
| − | Min Chen, Aaron Carass, Jiwon | + | [[Min|Min Chen]], {{iacl|~aaron|Aaron Carass}}, Jiwon Oh, Govind Nair, Dzung L. Pham, Daniel S. Reich, and [[Prince|Jerry L. Prince]] |
{{TOCright}} | {{TOCright}} | ||
| − | |||
| − | |||
{{h3|Introduction}} | {{h3|Introduction}} | ||
| Line 12: | Line 10: | ||
The human spinal cord is a long thin cylindrical structure of the central nervous system (CNS) extending from the medulla oblongata to the lumbar vertebrae. It is the principal transmission pathway for neural signals between the brain and the rest of the body. The primary function of the spinal cord makes it of great importance in studying diseases that lead to deterioration in CNS function. In vivo magnetic resonance imaging (MRI) of the human spinal cord presents a unique diagnostic tool in studying the progression and characteristics of such neurological diseases. Often times a full or partial segmentation is required when doing this research, both processes require manual or semi-automatic segmentations which limit the scale of future projects and produces long delays between acquiring the data and completing the analysis. In this work we present a fully automated spinal cord segmentation algorithm that combines deformable registration with topology preserving intensity classification. In addition, we augment the framework with an intensity atlas that is used with deformable registration to allow the atlases to be properly initialized. Finally we present a rapid approach for generating necessary topology and statistical atlases from a single manual segmentation. | The human spinal cord is a long thin cylindrical structure of the central nervous system (CNS) extending from the medulla oblongata to the lumbar vertebrae. It is the principal transmission pathway for neural signals between the brain and the rest of the body. The primary function of the spinal cord makes it of great importance in studying diseases that lead to deterioration in CNS function. In vivo magnetic resonance imaging (MRI) of the human spinal cord presents a unique diagnostic tool in studying the progression and characteristics of such neurological diseases. Often times a full or partial segmentation is required when doing this research, both processes require manual or semi-automatic segmentations which limit the scale of future projects and produces long delays between acquiring the data and completing the analysis. In this work we present a fully automated spinal cord segmentation algorithm that combines deformable registration with topology preserving intensity classification. In addition, we augment the framework with an intensity atlas that is used with deformable registration to allow the atlases to be properly initialized. Finally we present a rapid approach for generating necessary topology and statistical atlases from a single manual segmentation. | ||
| − | |||
| − | '''Figure 1''' | + | |
| + | <div style="background: white; border: 2px solid rgb(150, 150, 150); padding: 2px; text-align: justify;"> | ||
| + | {|style="background:width=50%" | ||
| + | | | ||
| + | {| | ||
| + | | | ||
| + | |- | ||
| + | | align=center| [[Image:AMRS_Figure_1.png]] | ||
| + | |- | ||
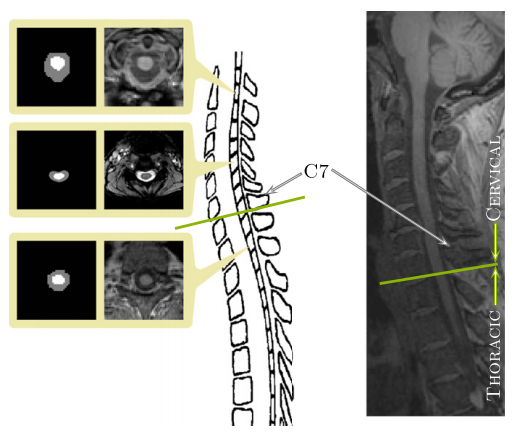
| + | | '''Figure 1:''' The center image is an illustration of a spinal cord. The left hand column shows (center) magnetization transfer-prepared T2*-weighted gradient-echo and (top and bottom) t1-weighted axial cross-sections of spinal cord MRIs and corresponding manual segmentations. | ||
| + | |- | ||
| + | |} | ||
| + | |} | ||
| + | </div> | ||
{{h3|Method}} | {{h3|Method}} | ||
| − | |||
The topology-preserving, anatomy-driven segmentation (TOADS) algorithm provides the main model for out segmentation approach. It is a fuzzy c-means (FCM) based intensity classification algorithm that is capable of preserving the digital topology of the anatomy being segmented. The flexibility of the TOADS algorithm allows the model to be adapted for the spinal cord; however there are several limitations in the existing framework. | The topology-preserving, anatomy-driven segmentation (TOADS) algorithm provides the main model for out segmentation approach. It is a fuzzy c-means (FCM) based intensity classification algorithm that is capable of preserving the digital topology of the anatomy being segmented. The flexibility of the TOADS algorithm allows the model to be adapted for the spinal cord; however there are several limitations in the existing framework. | ||
| Line 26: | Line 35: | ||
| − | [[Image:AMRS_Figure_2.png ]] | + | <div style="background: white; border: 2px solid rgb(150, 150, 150); padding: 2px; text-align: justify;"> |
| − | + | {|style="background: width=50%" | |
| − | + | | | |
| − | '''Figure 2''' | + | {| |
| − | the shape and curvature of the spinal cord in the images. | + | | |
| + | |- | ||
| + | | align= center| [[Image:AMRS_Figure_2.png ]] | ||
| + | |- | ||
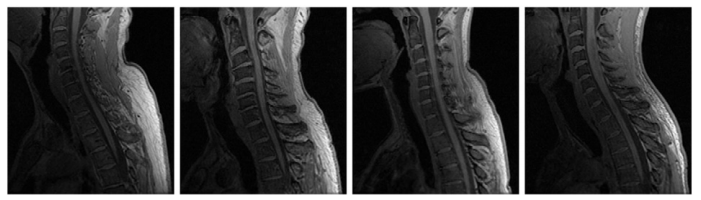
| + | | '''Figure 2:''' Sagittally acquired T1-weighted MR slices of the spinal cord from four different healthy subjects at approximately the same field of view. This demonstrates the wide variability in the shape and curvature of the spinal cord in the images. | ||
| + | |- | ||
| + | |} | ||
| + | |} | ||
| + | </div> | ||
| Line 39: | Line 56: | ||
But that is not all the tinkering required to directly apply TOADS for spinal cord segmentation. The original TOADS relies on a rigid initialization, which cannot fully capture the variability of the spinal cord. To address the problem we replace the rigid alignment step with a deformable registration. We introduce an intensity atlas into the TOADs framework in order to cut down on unreliability due to the segmentation. We also introduced a dynamic approach for initializing the topology atlas. Instead of applying the learned deformation to all three objects in the atlas, we only apply it to the spinal cord object. The other two objects are automatically added back after the spinal cord object has been deformed. | But that is not all the tinkering required to directly apply TOADS for spinal cord segmentation. The original TOADS relies on a rigid initialization, which cannot fully capture the variability of the spinal cord. To address the problem we replace the rigid alignment step with a deformable registration. We introduce an intensity atlas into the TOADs framework in order to cut down on unreliability due to the segmentation. We also introduced a dynamic approach for initializing the topology atlas. Instead of applying the learned deformation to all three objects in the atlas, we only apply it to the spinal cord object. The other two objects are automatically added back after the spinal cord object has been deformed. | ||
| + | <div style="background: white; border: 2px solid rgb(150, 150, 150); padding: 2px; text-align: justify;"> | ||
| + | {|style="background: width=50%;" | ||
| + | | | ||
| + | {| | ||
| + | | | ||
| + | |- | ||
| + | |align=center| [[Image:AMRS_Figure_4.png]] | ||
| + | |- | ||
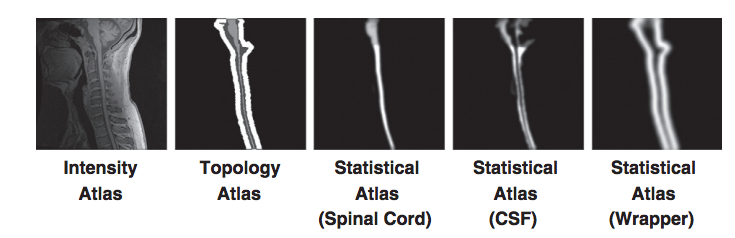
| + | | '''Figure 3:''' An example of the intensity, topology (spinal cord in light gray, CSF in dark gray, and wrapper in white) and statistical atlases constructed from a T1-weighted MRI. | ||
| + | |- | ||
| + | |} | ||
| + | |} | ||
| + | </div> | ||
| − | |||
| − | + | Our introduction of deformable registration into the TOADs algorithm also helps address potential problems. A major deficiency with existing methods for spinal cord segmentation is their inflexibility when facing very different datasets (particularly ones not used in the design of the algorithm. To overcome it we describe an automatic process for generating the necessary topology and statistical atlases from a single manual segmentation of an image from the desired dataset. This takes advantage of TOADs robustness to initialization errors, and the simple topology of the spinal cord. | |
| − | |||
| − | |||
| − | Our introduction of deformable registration into the TOADs algorithm also helps address potential problems. A major deficiency with existing methods for spinal cord segmentation is their inflexibility when facing very different datasets ( | ||
For our topology atlas construction we follow an approach similar to that of Bazin and Pham. We start by a manual segmentation of our intensity atlas and fix any topology errors that break our model. But our task is greatly simplified due to the dynamic initialization approach. Since all the objects in our atlas are dynamically built from just the spinal cord object, we only need to correct the topology for that single object. In addition, since the spinal cord in our model has spherical topology, this correction can be performed automatically using a simple algorithm | For our topology atlas construction we follow an approach similar to that of Bazin and Pham. We start by a manual segmentation of our intensity atlas and fix any topology errors that break our model. But our task is greatly simplified due to the dynamic initialization approach. Since all the objects in our atlas are dynamically built from just the spinal cord object, we only need to correct the topology for that single object. In addition, since the spinal cord in our model has spherical topology, this correction can be performed automatically using a simple algorithm | ||
| − | + | :# Find the largest connected component in the foreground. | |
| − | + | :# Set all smaller connected components in the foreground to background | |
| − | + | :# Find the largest connected component in the background | |
| − | + | :# Set all smaller connected components in the background to foreground. | |
| − | |||
| − | |||
| − | |||
This allows for the topology atlas for our method to be constructed quickly and automatically from a single segmentation. | This allows for the topology atlas for our method to be constructed quickly and automatically from a single segmentation. | ||
| Line 61: | Line 84: | ||
{{h3|Materials}} | {{h3|Materials}} | ||
| − | |||
Our algorithm was applied to two datasets having different population characteristics, MR protocols and scanners, and fields of view. | Our algorithm was applied to two datasets having different population characteristics, MR protocols and scanners, and fields of view. | ||
| Line 67: | Line 89: | ||
MT cohort: The second dataset used in our experiments consisted of 238 MRIs of the cervical spinal cord, acquired from the C2-C6 vertebrae. The scans were performed with a 3 Tesla Philips Intera scanner using body coil excitation and two element phased array surface coil reception. The images were magnetization transfer (MT) prepared T2-weighted gradient echoes, using an MT prepulse applied at 1.5 kHz off resonance. | MT cohort: The second dataset used in our experiments consisted of 238 MRIs of the cervical spinal cord, acquired from the C2-C6 vertebrae. The scans were performed with a 3 Tesla Philips Intera scanner using body coil excitation and two element phased array surface coil reception. The images were magnetization transfer (MT) prepared T2-weighted gradient echoes, using an MT prepulse applied at 1.5 kHz off resonance. | ||
| + | |||
{{h3|Results}} | {{h3|Results}} | ||
| − | [[Image:ARMS_Figure_8.png ]] | + | <div style="background: white; border: 2px solid rgb(150, 150, 150); padding: 2px; text-align: justify;"> |
| − | + | {|style="background: width=50%;" | |
| − | '''Figure 4''' | + | | |
| + | {| | ||
| + | | | ||
| + | |- | ||
| + | |align=center| [[Image:ARMS_Figure_8.png ]] | ||
| + | |- | ||
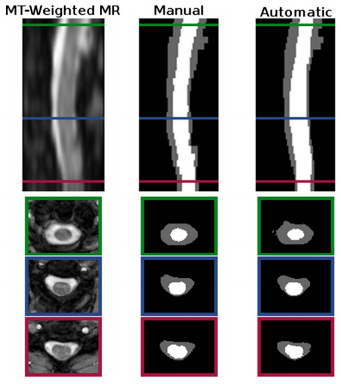
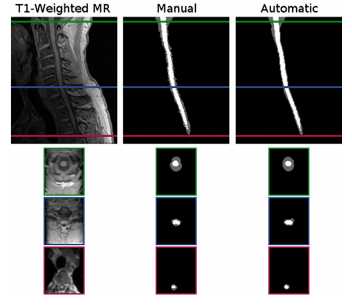
| + | | '''Figure 4:''' Cropped example of a MT-prepared T2*-weighted MRI segmentation by a human rater in comparison to the result from our algorithm. Shown are one sagittal and three axial views. The colored border around the axial slices denotes the respective cross-section within the sagittal image. The Dice coefficients between the shown manual and automatic segmentations are 0.91 for the spinal cord (white) and 0.86 for the CSF (gray). | ||
| + | |- | ||
| + | |} | ||
| + | |} | ||
| + | </div> | ||
| Line 81: | Line 114: | ||
Statistical atlas construction parameters: The impact of the two statistical atlas construction approached were evaluated by repeating our algorithm on five images from each cohort, while using atlases from both approaches with increasing kernel sizes ([[Image:ARMS_"o".png ]]) for the gaussian smoothing. In general [[Image:ARMS_"o".png ]] can be seen as a parameter for controlling the capture range of the statistical atlas. For the registration approach, the best performance was achieved without any smoothing ([[Image:ARMS_"o".png ]] = 0). However, for our single segmentation approach, smoothing with [[Image:ARMS_"o".png ]] = 1 was necessary to achieve the best performance. Both approaches had roughly the same performance at their respective optimal configurations, with our single segmentation approach performing slightly better in the CSF for the t1 data. | Statistical atlas construction parameters: The impact of the two statistical atlas construction approached were evaluated by repeating our algorithm on five images from each cohort, while using atlases from both approaches with increasing kernel sizes ([[Image:ARMS_"o".png ]]) for the gaussian smoothing. In general [[Image:ARMS_"o".png ]] can be seen as a parameter for controlling the capture range of the statistical atlas. For the registration approach, the best performance was achieved without any smoothing ([[Image:ARMS_"o".png ]] = 0). However, for our single segmentation approach, smoothing with [[Image:ARMS_"o".png ]] = 1 was necessary to achieve the best performance. Both approaches had roughly the same performance at their respective optimal configurations, with our single segmentation approach performing slightly better in the CSF for the t1 data. | ||
| − | [[Image:ARMS_Figure_9.png ]] | + | <div style="background: white; border: 2px solid rgb(150, 150, 150); padding: 2px; text-align: justify;"> |
| − | + | {|style="background: width=50%;" | |
| − | '''Figure 5''' | + | | |
| − | + | {| | |
| + | |- | ||
| + | | align=center| [[Image:ARMS_Figure_9.png ]] | ||
| + | |- | ||
| + | | '''Figure 5:''' Cropped example of a T1-weighted MRI segmentation by a human rater in comparison to the result from our algorithm. Shown are one sagittal and three axial views. The colored border around the axial slices denotes the respective cross-section within the sagittal image. The Dice coefficients between the shown manual and automatic segmentations are 0.87 for the spinal cord (white) and 0.73 for the CSF (gray). | ||
| + | |- | ||
| + | |} | ||
| + | |} | ||
| + | </div> | ||
| Line 93: | Line 134: | ||
{{h3|Conclusion}} | {{h3|Conclusion}} | ||
| − | |||
MRI of the spinal cord presents many challenges such as noise and artifacts which make automatic segmentation of the spinal cord and CSF a difficult task. We have presented a topology preserving approach for addressing this problem and have shown its effectiveness for both accuracy and robustness. We also made an algorithm easily adapted to be optimized for different spinal cord images. Finally our incorporation of deformable registration into TOADs has implications that extend beyond our application in the spinal cord. Allowing the atlas to be initialized deformably opens the model for segmentation in essentially any anatomy and image contrast where a successful registration can be achieved. Naturally, a topology and statistical atlas will have to be built for the specific anatomy, but our contribution has greatly generalized the framework for other applications. An implementation of the presented segmentation method and atlas construction approach can be freely downloaded as part of the Java Image Science Toolkit (JIST) software package. | MRI of the spinal cord presents many challenges such as noise and artifacts which make automatic segmentation of the spinal cord and CSF a difficult task. We have presented a topology preserving approach for addressing this problem and have shown its effectiveness for both accuracy and robustness. We also made an algorithm easily adapted to be optimized for different spinal cord images. Finally our incorporation of deformable registration into TOADs has implications that extend beyond our application in the spinal cord. Allowing the atlas to be initialized deformably opens the model for segmentation in essentially any anatomy and image contrast where a successful registration can be achieved. Naturally, a topology and statistical atlas will have to be built for the specific anatomy, but our contribution has greatly generalized the framework for other applications. An implementation of the presented segmentation method and atlas construction approach can be freely downloaded as part of the Java Image Science Toolkit (JIST) software package. | ||
{{h3|Acknowledgments}} | {{h3|Acknowledgments}} | ||
| + | Funding for this work was supported in part by NIH/NINDS grant R01-NS070906, the Intramural Research Program of NINDS, and the National MS Society (NMSS). | ||
| − | |||
| + | {{h3|Publications}} | ||
| + | {{iacl-pub|author= M. Chen, A. Carass, J. Oh, G. Nair, D.L. Pham, D.S. Reich, and J.L. Prince|title=Automatic Magnetic Resonance Spinal Cord Segmentation with Topology Constraints for Variable Fields of View|jrnl=ni|number=83:1051-1062|when=2013|doi=10.1016/j.neuroimage.2013.07.060}} | ||
| − | {{ | + | {{iacl-pub|author= M. Chen, A. Carass, J.L. Cuzzocreo, P. Bazin, D.S. Riech, and J.L. Prince|title=Topology preserving automatic segmentation of the spinal cord in magnetic resonance images|conf=isbi2011}} |
| − | + | {{iacl-pub|author= B.C. Lucas, J.A. Bogovic, A. Carass, P. Bazin, J.L. Prince, D.L. Pham, and B.A. Landman|title=The Java Image Science Toolkit (JIST) for Rapid Prototyping and Publishing of Neuroimaging Software|jrnl=Neuroinformatics|number=8(1):5-17|when=2010|doi=10.1007/s12021-009-9061-2}} | |
| − | + | {{iacl-pub|author= M. Chen, A. Carass, B. Wheeler, X. Liu, and J.L. Prince|title=Multi-channel Enhancement of the Adaptive Base Algorithm|conf=hbm2010}} | |
Latest revision as of 00:42, 3 July 2022
Automatic magnetic resonance spinal cord segmentation
Min Chen, Aaron Carass, Jiwon Oh, Govind Nair, Dzung L. Pham, Daniel S. Reich, and Jerry L. Prince
Introduction
The human spinal cord is a long thin cylindrical structure of the central nervous system (CNS) extending from the medulla oblongata to the lumbar vertebrae. It is the principal transmission pathway for neural signals between the brain and the rest of the body. The primary function of the spinal cord makes it of great importance in studying diseases that lead to deterioration in CNS function. In vivo magnetic resonance imaging (MRI) of the human spinal cord presents a unique diagnostic tool in studying the progression and characteristics of such neurological diseases. Often times a full or partial segmentation is required when doing this research, both processes require manual or semi-automatic segmentations which limit the scale of future projects and produces long delays between acquiring the data and completing the analysis. In this work we present a fully automated spinal cord segmentation algorithm that combines deformable registration with topology preserving intensity classification. In addition, we augment the framework with an intensity atlas that is used with deformable registration to allow the atlases to be properly initialized. Finally we present a rapid approach for generating necessary topology and statistical atlases from a single manual segmentation.
Method
The topology-preserving, anatomy-driven segmentation (TOADS) algorithm provides the main model for out segmentation approach. It is a fuzzy c-means (FCM) based intensity classification algorithm that is capable of preserving the digital topology of the anatomy being segmented. The flexibility of the TOADS algorithm allows the model to be adapted for the spinal cord; however there are several limitations in the existing framework.
First we must make a set of topology and statistical atlases that are anatomically meaningful in the context of the spinal cord and that can handle all possible fields of view. Most spinal cord MRIs do not cover the entire cord which can result in artificial breaks in the topology where the image ends part way through the cord. This needs to be accounted for both during the construction and the initialization of the topology atlas. Second, TOADS operates based on the assumption that the brain images have been skull stripped prior to running the algorithm.This is clearly not possible in our case. Our primary goal is to separate the spinal cord and CSF from the rest of the image so we must work with the surrounding tissue in the MRI. This makes registering the topology atlas (a segmentation image) to the MRI highly unreliable as well as the varied curvature of the spinal cord prevents a rigid or even affine transformation from providing an adequate initialization.
|
But these problems have solutions. The topology atlas serves as the topological rule set for the objects being segmented in our algorithm. In our model for the spinal cord this atlas only contains three objects: the spinal cord with spherical topology, the CSF with a spherical shell topology, and a “wrapper object also with a spherical shell topology. The wrapper is a “catch all” object for any structures that immediately surround the spinal canal (vertebrae, surrounding muscles, ect.). The diversity of tissues encompassed in the wrapper allow it to cover a wide range of image intensities. Its primary purpose is to provide a boundary that prevents the CSF object from extending past the spinal canal. Any object outside the wrapper is treated as background. We represent the topological relationships between these objects with just two basic assumptions: that the spinal cord is completely surrounded by the CSF and that the union of the CSF and spinal cord is completely surrounded by the wrapper. In our atlas, the CSF forms a “cap” on the top and bottom of the spinal cord. While the caps are not anatomically correct, they are used because the field of view forces a cutoff at the superior and inferior edges of the image. The cap prevents the background and wrapper objects from being connected to the spinal cord. Without the caps, those objects could evolve in between the CSF and spinal cord, effectively separating the two objects. Once the caps have served their purpose they are removed at the end of the algorithm. This and the fact they are added outside the field of view means they do not interfere with the accuracy of the segmentation at the boundaries.
In addition to the topology atlas a statistical atlas is used to define probabilistic priors on the locations of objects in the topology atlas. This is made by taking multiple spinal cord MR images and deformably registering them to a common template. Manual segmentations of the structures in each MR image are then transformed using the same deformation. This provides an empirical calculation for the probability of each object occurring at each voxel in the template space.
But that is not all the tinkering required to directly apply TOADS for spinal cord segmentation. The original TOADS relies on a rigid initialization, which cannot fully capture the variability of the spinal cord. To address the problem we replace the rigid alignment step with a deformable registration. We introduce an intensity atlas into the TOADs framework in order to cut down on unreliability due to the segmentation. We also introduced a dynamic approach for initializing the topology atlas. Instead of applying the learned deformation to all three objects in the atlas, we only apply it to the spinal cord object. The other two objects are automatically added back after the spinal cord object has been deformed.
|
Our introduction of deformable registration into the TOADs algorithm also helps address potential problems. A major deficiency with existing methods for spinal cord segmentation is their inflexibility when facing very different datasets (particularly ones not used in the design of the algorithm. To overcome it we describe an automatic process for generating the necessary topology and statistical atlases from a single manual segmentation of an image from the desired dataset. This takes advantage of TOADs robustness to initialization errors, and the simple topology of the spinal cord.
For our topology atlas construction we follow an approach similar to that of Bazin and Pham. We start by a manual segmentation of our intensity atlas and fix any topology errors that break our model. But our task is greatly simplified due to the dynamic initialization approach. Since all the objects in our atlas are dynamically built from just the spinal cord object, we only need to correct the topology for that single object. In addition, since the spinal cord in our model has spherical topology, this correction can be performed automatically using a simple algorithm
- Find the largest connected component in the foreground.
- Set all smaller connected components in the foreground to background
- Find the largest connected component in the background
- Set all smaller connected components in the background to foreground.
This allows for the topology atlas for our method to be constructed quickly and automatically from a single segmentation.
Materials
Our algorithm was applied to two datasets having different population characteristics, MR protocols and scanners, and fields of view.
T1 Cohort: The first dataset used in our experiments consisted of MR images of the brain stem and spinal cord from the c1-T4 vertebrae acquired from seven patients diagnosed with multiple sclerosis (MS). Each image was acquired using a T1-weighted inversion recovery fast spoiled gradient recall (FSPGR) on a Tesla GE Signa scanner.
MT cohort: The second dataset used in our experiments consisted of 238 MRIs of the cervical spinal cord, acquired from the C2-C6 vertebrae. The scans were performed with a 3 Tesla Philips Intera scanner using body coil excitation and two element phased array surface coil reception. The images were magnetization transfer (MT) prepared T2-weighted gradient echoes, using an MT prepulse applied at 1.5 kHz off resonance.
Results
|
We perform several experiments to demonstrate the performance and applications of our spinal cord segmentation tool. Our first experiment evaluates the accuracy of our algorithm relative to human raters. It also considers the effect of our registration choice for initializing our atlases. We then evaluate the impact of our statistical atlas construction approach and the size of the gaussian smoothing kernel used in its construction. Lastly we perform a large scale evaluation using the MT cohort to establish the robustness and potential clinical relevance of our algorithm.
Segmentation comparison against manual raters: We evaluated our automated segmentation results against the seven images from the T1 cohort and the twenty from the MT cohort that have corresponding manual segmentations. The dice coefficient was calculated for the spinal cord, CSP, and the union of the two structures (i.e. the spinal canal). In general the algorithm was better on the MT cohort than the T1 cohort, particularly for the CSF. The better tissue contrast and smaller intensity inhomogeneities in the MT cohort images led to better results. While the automatic results were very similar to the manual segmentations for both cases, the TOADs regularization let the automatic results be overall smoother. The individual accuracy of each registration algorithm was also considered by looking at its ability to transfer the atlas segmentation to the target image through applying the learned deformation from the intensity atlas registration. We see from these results that ABA generally performed much better than SyN for both datasets. Hence, t was the only registration algorithm considered in the remaining experiments.
Statistical atlas construction parameters: The impact of the two statistical atlas construction approached were evaluated by repeating our algorithm on five images from each cohort, while using atlases from both approaches with increasing kernel sizes (![]() ) for the gaussian smoothing. In general
) for the gaussian smoothing. In general ![]() can be seen as a parameter for controlling the capture range of the statistical atlas. For the registration approach, the best performance was achieved without any smoothing (
can be seen as a parameter for controlling the capture range of the statistical atlas. For the registration approach, the best performance was achieved without any smoothing (![]() = 0). However, for our single segmentation approach, smoothing with
= 0). However, for our single segmentation approach, smoothing with ![]() = 1 was necessary to achieve the best performance. Both approaches had roughly the same performance at their respective optimal configurations, with our single segmentation approach performing slightly better in the CSF for the t1 data.
= 1 was necessary to achieve the best performance. Both approaches had roughly the same performance at their respective optimal configurations, with our single segmentation approach performing slightly better in the CSF for the t1 data.
|
Robustness in large scale processing: to evaluate the robustness of our method, the entire MT cohort was processed using the proposed algorithm, The results were manually inspected for clear failures, which we designated as segmentations with roughly less than 75% spinal cord overlap. out of 238 images only eight failures were identified (due to strong artifacts present in each image).
Overall, our evaluations show that the proposed method achieved high accuracy and robustness when compared against manual segmentations from two independent raters for two datasets. Also, one major advantage of our algorithm is its ability to be quickly and automatically adapted for use with different spinal cord MRI data. The Topology we designed has a rule set that allows the topology atlas to be automatically constructed by correcting the topology of the spinal cord object and dynamically generating the remaining structures. We have also provided an alternative approach for approximating the statistical atlas that provides roughly the same level of performance as an atlas generated through the standard registration, and can be superior for T1-weighted data, particularly for the CSF. The main advantage however is that now only a single manual segmentation is necessary to construct all the atlases required for our algorithm to be entirely tailored to a specific dataset.
Conclusion
MRI of the spinal cord presents many challenges such as noise and artifacts which make automatic segmentation of the spinal cord and CSF a difficult task. We have presented a topology preserving approach for addressing this problem and have shown its effectiveness for both accuracy and robustness. We also made an algorithm easily adapted to be optimized for different spinal cord images. Finally our incorporation of deformable registration into TOADs has implications that extend beyond our application in the spinal cord. Allowing the atlas to be initialized deformably opens the model for segmentation in essentially any anatomy and image contrast where a successful registration can be achieved. Naturally, a topology and statistical atlas will have to be built for the specific anatomy, but our contribution has greatly generalized the framework for other applications. An implementation of the presented segmentation method and atlas construction approach can be freely downloaded as part of the Java Image Science Toolkit (JIST) software package.
Acknowledgments
Funding for this work was supported in part by NIH/NINDS grant R01-NS070906, the Intramural Research Program of NINDS, and the National MS Society (NMSS).
Publications
- M. Chen, A. Carass, J. Oh, G. Nair, D.L. Pham, D.S. Reich, and J.L. Prince, "Automatic Magnetic Resonance Spinal Cord Segmentation with Topology Constraints for Variable Fields of View", NeuroImage, 83:1051-1062, 2013.

- M. Chen, A. Carass, J.L. Cuzzocreo, P. Bazin, D.S. Riech, and J.L. Prince, "Topology preserving automatic segmentation of the spinal cord in magnetic resonance images", Eighth IEEE International Symposium on Biomedical Imaging (ISBI 2011), Chicago, IL, March 30 - April 2, 2011.
- B.C. Lucas, J.A. Bogovic, A. Carass, P. Bazin, J.L. Prince, D.L. Pham, and B.A. Landman, "The Java Image Science Toolkit (JIST) for Rapid Prototyping and Publishing of Neuroimaging Software", Neuroinformatics, 8(1):5-17, 2010.

- M. Chen, A. Carass, B. Wheeler, X. Liu, and J.L. Prince, "Multi-channel Enhancement of the Adaptive Base Algorithm", 16th Annual Meeting of the Organization for Human Brain Mapping (HBM 2010), Barcelona, Spain, June 6-10, 2010.