Difference between revisions of "CRUISE"
(Removed broken link.) |
|||
| Line 1: | Line 1: | ||
| − | |||
{{c2|CRUISE:Cortical Reconstruction Using Implicit Surface Evolution}} | {{c2|CRUISE:Cortical Reconstruction Using Implicit Surface Evolution}} | ||
{{iacl|~xhan/|X. Han}}, D.L. Pham, D. Tosun, {{iacl|~rettmann/|M.E. Rettmann}}, B. Lucas, S. Roy, {{iacl|~chenyang/|C. Xu}}, and [[Prince|J.L. Prince]] | {{iacl|~xhan/|X. Han}}, D.L. Pham, D. Tosun, {{iacl|~rettmann/|M.E. Rettmann}}, B. Lucas, S. Roy, {{iacl|~chenyang/|C. Xu}}, and [[Prince|J.L. Prince]] | ||
Latest revision as of 00:41, 3 July 2022
X. Han, D.L. Pham, D. Tosun, M.E. Rettmann, B. Lucas, S. Roy, C. Xu, and J.L. Prince
Overview
Segmentation and representation of the human cerebral cortex from magnetic resonance (MR) images plays an important role in neuroscience and medicine. A successful cortical reconstruction method must be robust to various imaging artifacts and produce anatomically meaningful and consistent cortical representations. In this work, we improve upon our previous efforts on central cortical surface reconstruction by addressing a few major limitations and introducing several novel developments. The resulting method, which we call CRUISE, is fast and numerically stable, and yields accurate brain surface reconstructions that are guaranteed to be topologically correct and free from self-intersections. (Download the software)
Introduction
Geometrically, the cerebral cortex is a thin, folded sheet of gray matter (GM) that is 1–5 mm thick. The cortical GM is bounded by the cerebrospinal fluid (CSF) on the outside, forming the pial cortical surface, and by the white matter (WM) on the inside, forming the inner cortical surface. It is useful to define the central cortical surface as well, which lies at roughly the geometric center between the inner and pial surfaces and gives an overall 2-D approximation to the 3-D cortical sheet. Finding the three surfaces enables the visualization and study of the sulcal and gyral patterns of an individual subject, and allows morphometric measurements such as cortical volume, surface area, cortical thickness, and sulcal depth. These measures provide valuable information about the cortical characteristics of both normal development and pathological diseases. Correspondences between cortical reconstructions from different subjects can also be used for image registration, digital atlas labeling, and population-based probabilistic atlas generation. In addition, cortical reconstruction is important for functional brain mapping, surgical planning, and cortical unfolding or flattening.
Cortical reconstruction is a step beyond pure segmentation that only classifies the image pixels as belonging to cortical GM or not. An accurate cortical reconstruction must generate a geometric representation of the cortex that is consistent with the true geometry of the brain cortex, complete with multiple lobes, gyral folds, and narrow sulci. In addition, a correct cortical surface reconstruction must have the correct spherical topology and be a valid 2-D manifold without self-intersections. This task is made difficult because of limitations in image quality, especially due to various imaging artifacts such as image noise, partial volume effects, and intensity inhomogeneities. To overcome these difficulties and get successful cortical reconstructions, the CRUISE method we developed systematically combines a robust fuzzy tissue classification algorithm, an efficient topology correction method, and a topology-preserving self-intersection free geometric deformable surface model.
Method and Results
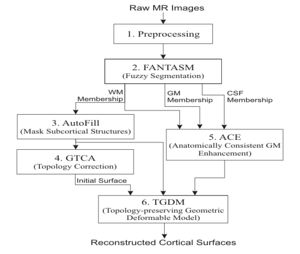
The CRUISE method can be summarized using the following block diagram. Results of applying each step of the method to a sample data set will be shown below.
- Preprocessing
This step mainly performs data interpolation and "skull-stripping", which is the same as in the previous method.
- Fuzzy segmentation
The second step of CRUISE applies a fuzzy tissue classification to identify the spatial distribution of GM, WM, and CSF within the image volume. The classification method, called FANTASM, applies a novel "fuzzy" spatial regularization to reduce the effects of image noise. It also compensates for MR intensity inhomogeneities by estimating a gain field along with the segmentation.
- Automatic editing of WM membership function (AutoFill)
Autofill consists of a sequence of image processing operations that automatically fills the ventricles and subcortical GM structures within the WM membership function. After AutoFill, the isosurface of WM membership function will produce a good approximation of the inner cortical surface, at least in geometry.
- Topology correction of WM isosurface
Because of noise and partial volume averaging, an isosurface directly generated from the AutoFill processed WM membership function typically contains hundreds of handles. We apply in this step the Graph-based topology correction algorithm (GTCA) that was previously developed in our group in order to remove all the handles from the WM isosurface. Like other major topology correction methods proposed in the literature, GTCA was originally designed for the processing of binarized volumes only. A small trick is introduced in this work to improve GTCA so that the subvoxel accuracy of the original isosurface can be kept after the topology correction.
- Anatomically consistent GM enhancement (ACE)
ACE applies a weighted skeleton computation to edit the original GM membership function in order to get a GM representation that has evidence of sulci where it might not otherwise exist due to the partial volume effect. As shown in Fig.5, in most cases when sulcal banks are back-to-back and no CSF was apparent in the original GM membership image, ACE now produces a noticeable gap between the banks in the modified membership image. There are also "gentle reinforcement" of weak sulci, preserving the location of the sulcal gap and the nonuniform cortical thickness on opposite banks.
- Nested cortical surface reconstruction
Finally, we apply three Topology-preserving geometric deformable surface model (TGDM) to find the three cortical surfaces in sequence. An additional nesting constraint is imposed during the implementation to ensure that the extracted surfaces are properly nested (the central inside the pial, and the inner inside the central). Fig. 6 shows the reconstructed surfaces overlaid on various cross-sections of the original MR image.
Conclusion
We have developed a new approach for brain cortex segmentation that reconstructs all three key representative surfaces of the cortex. As having been verified by validation studies, the CRUISE method is computational fast and produces surfaces that are geometrically accurate, have the correct topology, and do not self-intersect or mutually intersect. CRUISE provides a full cortex characterization in a nearly fully automatic fashion, which makes it possible to conduct sophisticated neuroanatomical studies that involve large amount of imaging data. Future work involves the elimination of few manual interactions in the preprocessing step and more thorough evaluation of the method accuracy. Applying the CRUISE method to the processing of over a thousand data set is also undergoing.
Acknowledgment
This work is supported in part by NSF/ERC Grant CISST9731748 and in part by NIH/NINDS Grant R01NS37747.
Publications
C. XU and J.L. Prince, "Snakes, shapes, and gradient vector flow", IEEE Transactions on Image Processing, 359-369, March, 1998
C. Xu, D. L. Pham, M. E. Rettmann, D. N. Yu, and J. L. Prince, "Reconstruction of the human cerebral cortex from magnetic resonance images," IEEE Transactions on Medical Imaging, 18(6), pp. 467-480, June, 1999.
X. Han, C. Xu, M. E. Rettmann, and J. L. Prince, "Automated segmentation editing for cortical surface reconstruction", Proc. SPIE Med. Imag., vol. 4322, pp. 194-203, 2001.
D. Tosun and J. L. Prince, "Hemispherical map for the human brain cortex," in Proc. SPIE Medical Imaging, vol. 4322, Paper 31, San Diego, February 2001.
D. L. Pham, "Robust fuzzy segmentation of magnetic resonance images", Proc. 14th IEEE Symp. Comput. Based Med. Sys. (CBMS2001), pp. 127-131, 2001.
X. Han, C. Xu, and J. L. Prince, "A topology preserving deformable model using level set," in Proc. IEEE Conf. CVPR 2001, vol. II, pages 765--770, Kauai, HI, Dec 2001.
X. Han, C. Xu, D. Tosun, and J. L. Prince, "Cortical surface reconstruction using a topology preserving geometric deformable model," in Proc. 5th IEEE Workshop MMBIA 2001, pages 213--220, Kauai, HI, Dec 2001.
X. Han, C. Xu, U. Braga-Neto, and J. L. Prince, "Graph-based topology correction for brain cortex segmentation," in Proc. XVIIth Int. Conf. Information Processing in Medical Imaging, June 2001.
D. L. Pham, X. Han, M. E. Rettmann, C. Xu, D. Tosun, S. M. Resnick, and J. L. Prince, "New approaches for measuring changes in the cortical surface using an automatic reconstruction algorithm", in Proc. SPIE Med. Imag., vol. 4684, pp. 191-200, 2002.
X. Han, C. Xu, U. Braga-Neto, and J. L. Prince, "Topology correction in brain cortex segmentation using a multiscale, graph-based approach," IEEE Trans. Med. Imag., 21(2): 109--121, 2002.
X. Han, C. Xu, and J.L. Prince, "A topology preserving geometric deformable model and its application in brain cortical surface reconstruction," in Geometric Level Set Methods in Imaging, Vision, and Graphics, S. Osher and N. Paragios, Eds. Springer Verlag, 2003.
X. Han, C. Xu, and J.L. Prince, "A topology preserving level set method for geometric deformable models," IEEE Trans. PAMI, 25(6):755--768, 2003.
X. Han, D. L. Pham, D. Tosun, M. E. Rettmann, C. Xu, and J.L. Prince, "CRUISE: Cortical reconstruction using implicit surface evolution," NeuroImage, Vol 23:997--1012, 2004.
D. Tosun, M.E. Rettmann, D.Q. Naiman, S.M. Resnick, M.A. Kraut, and J.L. Prince, "Cortical Reconstruction Using Implicit Surface Evolution: Accuracy and Precision Analysis," NeuroImage, Vol 29(3):838-852, 2005.