GVF Snake

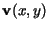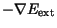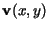After we compute ${\bf v}(x,y)$, we replace the potential force $- \nabla E _{\rm ext}$ in the dynamic snake equation of (7) by ${\bf v}(x,y)$, yielding

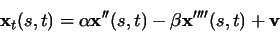$${\bf x}_t(s,t) = \alpha {\bf x}''(s,t) - \beta {\bf x}''''(s,t) + {\bf v}$$ (13)

We call the parametric curve solving the above dynamic equation as a GVF snake. This equation is solved in similar fashion to the traditional snake -- i.e., by discretization and iterative solution.